题目内容
19.已知:$\frac{1}{a_{n+1}}$=$\sqrt{3+\frac{1}{a_{n}^{2}}}$,(n∈N*),且a1=1,an>0.(1)求证:{$\frac{1}{a_{n}^{2}}$}为等差数列.
(2)求出通项公式.
分析 (1)把已知的数列递推式两边平方,即可证得{$\frac{1}{a_{n}^{2}}$}为等差数列;
(2)由(1)中的等差数列求出通项公式,进一步可得数列{an}的通项公式.
解答 (1)证明:由$\frac{1}{a_{n+1}}$=$\sqrt{3+\frac{1}{a_{n}^{2}}}$,得$\frac{1}{{{a}_{n+1}}^{2}}=3+\frac{1}{{{a}_{n}}^{2}}$,
即$\frac{1}{{{a}_{n+1}}^{2}}-\frac{1}{{{a}_{n}}^{2}}=3$,
又a1=1,∴$\frac{1}{{{a}_{1}}^{2}}=1$,
则数列{$\frac{1}{a_{n}^{2}}$}为以1为首项,以3为公差的等差数列;
(2)解:∵数列{$\frac{1}{a_{n}^{2}}$}为以1为首项,以3为公差的等差数列,
∴$\frac{1}{{{a}_{n}}^{2}}=1+3(n-1)=3n-2$,
则${{a}_{n}}^{2}=\frac{1}{3n-2}$,又an>0,
∴${a}_{n}=\sqrt{\frac{1}{3n-2}}$.
点评 本题考查了数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.

练习册系列答案
相关题目
9.函数f(x)=(x-2)ex的单调递增区间是( )
| A. | (-∞,1) | B. | ( 0,2 ) | C. | (1,+∞) | D. | (2,+∞) |
4.研究表明,成年人的身高和体重具有线性相关性,小明随机调查了五名成年人甲、乙、丙、丁、戊的身高和体重,得到的结果如下表所示,根据表格中的数据回答下列问题:
(1)从这五名成年人中任选两名做问卷调查,求选出的两名成年人的身高均超过170cm的概率;
(2)求体重y对身高x的线性回归方程y=bx+a,并据此预测身高为180cm的成年人的体重大约是多少?
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| 身高x(cm) | 166 | 170 | 172 | 174 | 178 |
| 体重y(kg) | 55 | 60 | 65 | 65 | 70 |
(2)求体重y对身高x的线性回归方程y=bx+a,并据此预测身高为180cm的成年人的体重大约是多少?
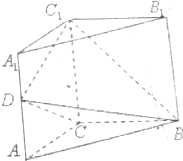 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{1}{2}$AA1,D是棱AA1上的动点.