题目内容
设f（x）=（1+et）x-e2t．其中x∈R，t为常数；集合M={x|f（x）＜0，x∈R}，则对任意实常数t，总有（ ）
| A、-3∉M，0∈M | B、-3∉M，0∉M | C、-3∈M，0∉M | D、-3∈M，0∈M |
分析：根据题意，判定x=0，和x=-3是否是集合M中的元素即可；
解答：解：根据题意，得f（x）=（1+et）x-e2t＜0，
当x=0时，f（x）=-e2t＜0，∴0∈M；
当x=-3时，f（x）=-3（1+et）-e2t=-[3（1+et）+e2t]＜0，∴-3∈M；
故选：D．
当x=0时，f（x）=-e2t＜0，∴0∈M；
当x=-3时，f（x）=-3（1+et）-e2t=-[3（1+et）+e2t]＜0，∴-3∈M；
故选：D．
点评：本题考查了元素与集合的关系，是基础题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
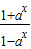且a≠1），函数y=g（x）的图象与函数y=f（x）图象关于直线x-y=0对称．
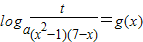在[2，6]上有实数解，求t的取值范围；
．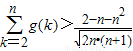