题目内容
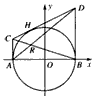
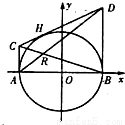
如图,过圆x2+y2=4与x轴的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R,
(1)求动点R的轨迹E的方程;
(2)过曲线E的右焦点F作直线l交曲线E于M、N两点,交y轴于P点,且记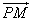 =λ1
=λ1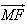 ,
, =λ2
=λ2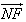 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.
(1)求动点R的轨迹E的方程;
(2)过曲线E的右焦点F作直线l交曲线E于M、N两点,交y轴于P点,且记
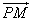 =λ1
=λ1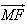 ,
, =λ2
=λ2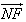 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值. 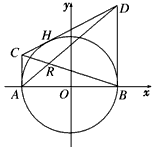
解:(1)设点H的坐标为(x0,y0),则x+y=4,
由题意可知y0≠0,且以H为切点的圆的切线的斜率为:- ,
,
故切线方程为:y-y0=- (x-x0),
(x-x0),
展开得x0x+y0y=x02+y02=4,
即以H为切点的圆的切线方程为:x0x+y0y=4,
∵A(-2,0),B(2,0),
将x=±2代入上述方程可得点C,D的坐标分别为C(-2, ),D(2,
),D(2, ),
),
则lAD: ,①,
,①,
及lBC: ,②
,②
将两式相乘并化简可得动点R的轨迹E的方程为:x2+4y2=4,即 +y2=1。
+y2=1。
(2)由(1)知轨迹E为焦点在x轴上的椭圆且其右焦点为F( ,0),
,0),
(ⅰ)当直线l的斜率为0时,M、N、P三点在x轴上,
不妨设M(2,0),N(-2,0),且P(0,0),
此时有|PM|=2,|MF|=2- ,|PN|=2,|NF|=2+
,|PN|=2,|NF|=2+ ,
,
所以λ1+λ2= ;
;
(ⅱ)当直线l的斜率不为0时,设直线MN的方程是:x=my+ (m≠0),
(m≠0),
则点P的坐标为(0,- ),
),
且设点M(x1,y1),N(x2,y2),
联立 消去x可得:(m2+4)y2+2
消去x可得:(m2+4)y2+2 my-1=0,
my-1=0,
则y1+y2= ,y1y2=
,y1y2= ,
,
λ1+λ2= =-8(定值).
=-8(定值).
由题意可知y0≠0,且以H为切点的圆的切线的斜率为:-
 ,
,故切线方程为:y-y0=-
 (x-x0),
(x-x0),展开得x0x+y0y=x02+y02=4,
即以H为切点的圆的切线方程为:x0x+y0y=4,
∵A(-2,0),B(2,0),
将x=±2代入上述方程可得点C,D的坐标分别为C(-2,
 ),D(2,
),D(2, ),
),则lAD:
 ,①,
,①,及lBC:
 ,②
,②将两式相乘并化简可得动点R的轨迹E的方程为:x2+4y2=4,即
 +y2=1。
+y2=1。(2)由(1)知轨迹E为焦点在x轴上的椭圆且其右焦点为F(
 ,0),
,0),(ⅰ)当直线l的斜率为0时,M、N、P三点在x轴上,
不妨设M(2,0),N(-2,0),且P(0,0),
此时有|PM|=2,|MF|=2-
 ,|PN|=2,|NF|=2+
,|PN|=2,|NF|=2+ ,
,所以λ1+λ2=
 ;
;(ⅱ)当直线l的斜率不为0时,设直线MN的方程是:x=my+
 (m≠0),
(m≠0),则点P的坐标为(0,-
 ),
),且设点M(x1,y1),N(x2,y2),
联立
 消去x可得:(m2+4)y2+2
消去x可得:(m2+4)y2+2 my-1=0,
my-1=0,则y1+y2=
 ,y1y2=
,y1y2= ,
,λ1+λ2=
 =-8(定值).
=-8(定值).
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
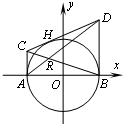 如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R.
如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R. (2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.
(2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.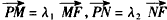 ,求证:λ1+λ2为定值。
,求证:λ1+λ2为定值。