题目内容
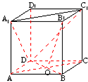 如图,O是长方体ABCD-A1B1C1D1底面对角线AC与BD的交点,求证:B1O∥平面A1C1D.
如图,O是长方体ABCD-A1B1C1D1底面对角线AC与BD的交点,求证:B1O∥平面A1C1D.分析:证明B1O∥O1D,利用线面平行的判定定理,即可证得结论.
解答: 证明:连A1C1交B1D1于O1,连DO1,
证明:连A1C1交B1D1于O1,连DO1,
∵O1B1∥DO,O1B1=DO,
∴O1B1OD为平行四边形,
∴B1O∥O1D
∵BO1?平面A1C1D,O1D?平面A1C1D,
∴B1O∥平面A1C1D.
 证明:连A1C1交B1D1于O1,连DO1,
证明:连A1C1交B1D1于O1,连DO1,∵O1B1∥DO,O1B1=DO,
∴O1B1OD为平行四边形,
∴B1O∥O1D
∵BO1?平面A1C1D,O1D?平面A1C1D,
∴B1O∥平面A1C1D.
点评:本题考查线面平行,考查学生分析解决问题的能力,正确运用线面平行的判定定理是关键.

练习册系列答案
相关题目
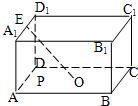 例2:如图,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1,对于点P的轨迹,下列说法正确的是( )
例2:如图,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1,对于点P的轨迹,下列说法正确的是( )A、离心率为
| ||||
B、离心率为
| ||||
| C、一段抛物线 | ||||
| D、半径等于1的圆 |
 (2012•安徽)如图,长方体ABCD-A1B1C1D1 中,底面A1B1C1D1 是正方形,O是BD的中点,E是棱AA1上任意一点.
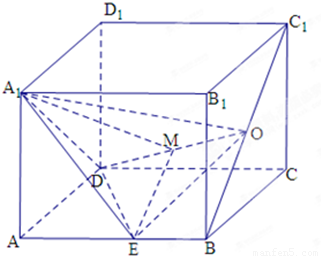
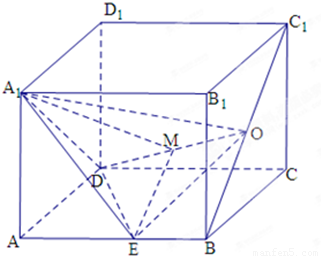
(2012•安徽)如图,长方体ABCD-A1B1C1D1 中,底面A1B1C1D1 是正方形,O是BD的中点,E是棱AA1上任意一点. 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.