题目内容
设
是定义在
上奇函数，且当
时，
，求函数的解析式
【解析】
试题分析：根据函数
是定义在
上的奇函数，图像关于原点对称，解析式满足
，所以
，且已知
时的解析式，那么当
时的解析式，可由
时，
表示，同时当时，
，所以当时，得到：
，综上得到所求的函数的解析式.
试题解析：（1）是定义在上奇函数，
，
（3分）
（2）当
时，
，
是定义在上奇函数，
（10分）
（12分）
考点：1.函数的奇偶性；2.转化法.
练习册系列答案
相关题目
。
在
是增函数，求
的取值范围；
且
时，
恒成立，求
的取值范围.
，因为
是实数，所以
”你认为这个推理（ ）．
B.
C.
D.
的函数
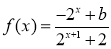是奇函数。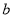
的值；
的单调性;
，不等式
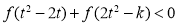恒成立，求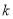
的取值范围．
，
，
，则
从小到大的顺序是 
元，年用电量为
亿千瓦时．本年度计划将电价调至
之间，经测算，若电价调至
元，则本年度新增用电量
（亿千瓦时）与
元成反比例．又当
时，
.
元，则电价调至多少时，本年度电力部门的收益将比上年增加
？[收益＝用电量×（实际电价－成本价）]
表同一函数的是（ ）
在坐标轴上，离心率为
，
.
在双曲线上，求证：
；
，求
的面积.