题目内容
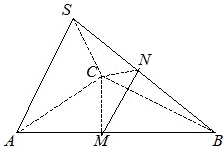 如图,在三棱锥S-ABC中,底面ABC是边长为4的正三角形,侧面SAC⊥底面ABC,SA=SC=2
如图,在三棱锥S-ABC中,底面ABC是边长为4的正三角形,侧面SAC⊥底面ABC,SA=SC=2| 3 |
(Ⅰ)求证:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小.
分析:(解法一)
(Ⅰ)由题意取AC的中点O,连接OS则SO⊥平面ABC,AC⊥SO;再由三垂线定理得AC⊥SB;
(Ⅱ)取OB的中点D,由SO⊥平面ABC和DN∥SO,得DN⊥平面ABC,作NE⊥CM交CM于E,
连接DE,再证DE⊥CM,则∠NED即为所求,在直角三角形中求解.
(解法二)
(Ⅰ)由题意建立空间直角坐标系,求
•
=0得AC⊥SB;
(Ⅱ)因SO⊥平面ABC,则
为平面ABC的法向量,求平面CMN的一个法向量
,再求两向量
夹角的余弦值.
(Ⅰ)由题意取AC的中点O,连接OS则SO⊥平面ABC,AC⊥SO;再由三垂线定理得AC⊥SB;
(Ⅱ)取OB的中点D,由SO⊥平面ABC和DN∥SO,得DN⊥平面ABC,作NE⊥CM交CM于E,
连接DE,再证DE⊥CM,则∠NED即为所求,在直角三角形中求解.
(解法二)
(Ⅰ)由题意建立空间直角坐标系,求
| AC |
| SB |
(Ⅱ)因SO⊥平面ABC,则
| SO |
| n |
夹角的余弦值.
解答: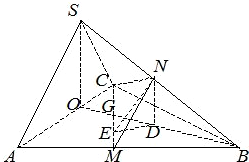 解:(Ⅰ)取AC的中点O,连接OS,OB.
解:(Ⅰ)取AC的中点O,连接OS,OB.
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥OB.
又∵平面SAC⊥平面ABC,且平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.故SB在平面ABC内的射影为OB,
∴AC⊥SB.(6分)
(Ⅱ) 取OB的中点D,作NE⊥CM交CM于E,连接DE,ND.
在△SOB中,N,D分别为SB,OB的中点,
∴DN∥SO.
∵SO⊥平面ABC,
∴DN⊥平面ABC,∴DN⊥CM,∵NE⊥CM,∴CM⊥平面DNE
∴DE⊥CM.
故∠NED为二面角N-CM-B的平面角.(9分)
设OB与CM交于G,则G为△ABC的中心,
∴GD=
GB.
又∵DE⊥CM,BM⊥CM,
∴DE∥MB,∴DE=
MB=
.
在△SAC中可得SO=2
,在△SOB中,ND=
SO=
,
在Rt△NDE中,tanNED=
=2
.
∴∠NED=arctan2
.∴二面角N-CM-B的大小为arctan2
.(14分)
(解法二):(Ⅰ)取AC的中点O,连接OS,OB.
∵SA=SC,AB=BC,∴AC⊥SO,AC⊥OB.
又平面SAC⊥平面ABC,且平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.
如图所示建立空间直角坐标系O-xyz,
A(2,0,0),B(0,2
,0),C(-2,0,0),S(0,0,2
),M(1,
,0),N(0,
,
).
∴
=(-4,0,0),
=(0,2
,-2
).
则
•
=0,
∴AC⊥SB.(6分)
(Ⅱ)由(Ⅰ)得
=(3,
,0),
=(-1,0,
).
设
=(x,y,z)为平面CMN的一个法向量,
取z=1,得x=
,y=-
,∴n=(
,-
1).
又
=(0,0,2
)为平面ABC的法向量,
∴cos<n•
>=
=
.
∴二面角N-CM-B的大小为arccos
.(14分)
 解:(Ⅰ)取AC的中点O,连接OS,OB.
解:(Ⅰ)取AC的中点O,连接OS,OB.∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥OB.
又∵平面SAC⊥平面ABC,且平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.故SB在平面ABC内的射影为OB,
∴AC⊥SB.(6分)
(Ⅱ) 取OB的中点D,作NE⊥CM交CM于E,连接DE,ND.
在△SOB中,N,D分别为SB,OB的中点,
∴DN∥SO.
∵SO⊥平面ABC,
∴DN⊥平面ABC,∴DN⊥CM,∵NE⊥CM,∴CM⊥平面DNE
∴DE⊥CM.
故∠NED为二面角N-CM-B的平面角.(9分)
设OB与CM交于G,则G为△ABC的中心,
∴GD=
| 1 |
| 4 |
又∵DE⊥CM,BM⊥CM,
∴DE∥MB,∴DE=
| 1 |
| 4 |
| 1 |
| 2 |
在△SAC中可得SO=2
| 2 |
| 1 |
| 2 |
| 2 |
在Rt△NDE中,tanNED=
| ||
|
| 2 |
∴∠NED=arctan2
| 2 |
| 2 |
(解法二):(Ⅰ)取AC的中点O,连接OS,OB.
∵SA=SC,AB=BC,∴AC⊥SO,AC⊥OB.
又平面SAC⊥平面ABC,且平面SAC∩平面ABC=AC,
∴SO⊥平面ABC.
如图所示建立空间直角坐标系O-xyz,
A(2,0,0),B(0,2
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
∴
| AC |
| SB |
| 3 |
| 2 |
则
| AC |
| SB |
∴AC⊥SB.(6分)
(Ⅱ)由(Ⅰ)得
| CM |
| 3 |
| MN |
| 2 |

设
| n |
|
取z=1,得x=
| 2 |
| 6 |
| 2 |
| 6, |
又
| OS |
| 2 |
∴cos<n•
| OS |
n•
| ||
|n|•|
|
| 1 |
| 3 |
∴二面角N-CM-B的大小为arccos
| 1 |
| 3 |
点评:本题为一题多解的情况,一种是向量法,需要利用已有的垂直关系建立空间直角坐标系,向量的数量积来证垂直,求平面的法向量来求二面角的余弦值;另一种用垂直关系的定义和定理,三垂线定理来证明线线垂直、线面垂直,作出二面角O-AC-O1的平面角.向量法要简单些.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )