题目内容
已知圆M:(x+(1)(理22(1)文21(1))求点G的轨迹C的方程;
(2)(理22(2))过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设![]() ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程,若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程,若不存在,试说明理由.
(文21(2))直线l的方程为l:3x-2y-6=0,与曲线C交于A、B两点,O是坐标原点,且![]() ,求证:四边形OASB为矩形.
,求证:四边形OASB为矩形.
(1)解:(理22(1)文21(1)) GQ为NP的中垂线
GQ为NP的中垂线![]() |GP|=|GN|,
|GP|=|GN|,
∴|GN|+|GM|=|MP|=6.故G点的轨迹是以M、N为焦点的椭圆,其半长轴长a=3,半焦距c=![]() .
.
∴半短轴长b=2.∴点G的轨迹方程是![]() =1.
=1.
(2)(理22(2))解:∵![]() ,∴四边形OASB为平行四边形.若存在l使得|
,∴四边形OASB为平行四边形.若存在l使得|![]() |=|
|=|![]() |,则四边形OASB为矩形,∴
|,则四边形OASB为矩形,∴![]() =0.若l的斜率不存在,直线l的方程为x=2,
=0.若l的斜率不存在,直线l的方程为x=2,
由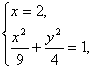 得
得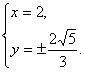 .∴
.∴![]() =
=![]() >0,与
>0,与![]() =0矛盾,故l的斜率存在.设l的方程为y=k(x-2),A(x1,y1),B(x2,y2),
=0矛盾,故l的斜率存在.设l的方程为y=k(x-2),A(x1,y1),B(x2,y2),
由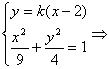 (9k2+4)x2-36k2x+36(k2-1)=0.
(9k2+4)x2-36k2x+36(k2-1)=0.
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,①
,①
y1y2=[k(x1-2)][k(x2-2)]=k2[x1x2-2(x1+x2)+4]=![]() .②
.②
把①②代入x1x2+y1y2=0,得k=±![]() .∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等.
.∴存在直线l:3x-2y-6=0或3x+2y-6=0使得四边形OASB的对角线相等.
(文21(2))证明:∵![]() ,∴四边形OASB为平行四边形.
,∴四边形OASB为平行四边形.
设A(x1,y1),B(x2,y2),由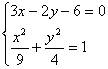 =1
=1![]() x2-81x+45=0.
x2-81x+45=0.
∴x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
∴![]() =x1x2+y1y2=x1x2+
=x1x2+y1y2=x1x2+![]() (x1-2)(x2-2)=
(x1-2)(x2-2)=![]() x1x2
x1x2![]() (x1+x2)+9=
(x1+x2)+9=![]() +9=0.∴四边形OASB为矩形.
+9=0.∴四边形OASB为矩形.

练习册系列答案
相关题目