题目内容
设函数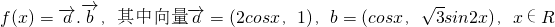
(1)求函数f(x)的单调减区间;
(2)若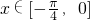 ,求函数f(x)的值域.
,求函数f(x)的值域.
解:(1)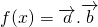 =2cos2x+
=2cos2x+ sin2x
sin2x
= sin2x+cos2x+1=2sin(2x+
sin2x+cos2x+1=2sin(2x+ )+1
)+1
令 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,得kπ+
+2kπ,得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
因此,函数f(x)的单调减区间是[kπ+ ,kπ+
,kπ+ ],k∈Z,
],k∈Z,
(2)当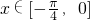 时,2x+
时,2x+ ∈[-
∈[- ,
, ].
].
∴2sin(2x+ )∈[-
)∈[- ,
, ],得y=2sin(2x+
],得y=2sin(2x+ )+1∈[-
)+1∈[- +1,2]
+1,2]
即函数f(x)在区间 的值域是[-
的值域是[- +1,2].
+1,2].
分析:(1)根据平面向量数量积的坐标运算公式,结合二倍角的三角公式化简整理,得f(x)═2sin(2x+ )+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间;
)+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间;
(2)根据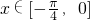 易得2x+
易得2x+ ∈[-
∈[- ,
, ].结合正弦函数的图象与性质,得2sin(2x+
].结合正弦函数的图象与性质,得2sin(2x+ )∈[-
)∈[- ,
, ],由此不难得到函数f(x)在区间
],由此不难得到函数f(x)在区间 的值域.
的值域.
点评:本题以平面向量的坐标运算为载体,着重考查了二倍角的三角函数公式、辅助角公式和三角函数的图象与性质等知识,属于基础题.
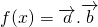 =2cos2x+
=2cos2x+ sin2x
sin2x=
 sin2x+cos2x+1=2sin(2x+
sin2x+cos2x+1=2sin(2x+ )+1
)+1令
 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,得kπ+
+2kπ,得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,因此,函数f(x)的单调减区间是[kπ+
 ,kπ+
,kπ+ ],k∈Z,
],k∈Z,(2)当
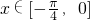 时,2x+
时,2x+ ∈[-
∈[- ,
, ].
].∴2sin(2x+
 )∈[-
)∈[- ,
, ],得y=2sin(2x+
],得y=2sin(2x+ )+1∈[-
)+1∈[- +1,2]
+1,2]即函数f(x)在区间
 的值域是[-
的值域是[- +1,2].
+1,2].分析:(1)根据平面向量数量积的坐标运算公式,结合二倍角的三角公式化简整理,得f(x)═2sin(2x+
 )+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间;
)+1.再根据正弦函数的单调区间的公式,解不等式可得函数f(x)的单调减区间;(2)根据
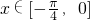 易得2x+
易得2x+ ∈[-
∈[- ,
, ].结合正弦函数的图象与性质,得2sin(2x+
].结合正弦函数的图象与性质,得2sin(2x+ )∈[-
)∈[- ,
, ],由此不难得到函数f(x)在区间
],由此不难得到函数f(x)在区间 的值域.
的值域.点评:本题以平面向量的坐标运算为载体,着重考查了二倍角的三角函数公式、辅助角公式和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 设函数
设函数 (2009•成都模拟)设函数
(2009•成都模拟)设函数
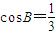 ,
,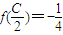 ,且C为锐角,求sinA的值.
,且C为锐角,求sinA的值.