题目内容
已知椭圆C的中心在原点,焦点在x轴上,离心率是 ,且左顶点与右焦点F的距离为3.
,且左顶点与右焦点F的距离为3.(1)求椭圆C的方程;
(2)过点F的直线交椭圆C于A、B两点,A、B在右准线l上的射影分别为M、N.求证:AN与BM的交点在x轴上.
【答案】分析:(1)设椭圆C的方程为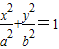 (a>b>0),由题意得
(a>b>0),由题意得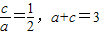 ,可得a,c,再由a2=b2+c2可得b;
,可得a,c,再由a2=b2+c2可得b;
(2):①当AB垂直于x轴时,易证明;②当AB不垂直于x轴时,设直线AB的方程为y=k(x-1),代入椭圆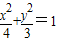 ,得(4k2+3)x2-8k2x+(4k2-12)=0,设A(x1,y1),B(x2,y2),写出直线AN、BM的方程联立,及韦达定理可求得AN与BM的交点,由其坐标可得结论;
,得(4k2+3)x2-8k2x+(4k2-12)=0,设A(x1,y1),B(x2,y2),写出直线AN、BM的方程联立,及韦达定理可求得AN与BM的交点,由其坐标可得结论;
解答:(1)解:设椭圆C的方程为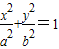 (a>b>0),
(a>b>0),
则由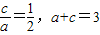 ,得a=2,c=1,b2=3,
,得a=2,c=1,b2=3,
所以椭圆C的方程为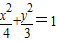 ;
;
(2)证明:①当AB垂直于x轴时,AB的坐标分别为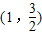 ,
,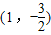 ,AN与BM的交点为
,AN与BM的交点为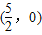 在x轴上.
在x轴上.
②当AB不垂直于x轴时,设直线AB的方程为y=k(x-1),
代入椭圆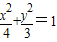 ,得(4k2+3)x2-8k2x+(4k2-12)=0,
,得(4k2+3)x2-8k2x+(4k2-12)=0,
设A(x1,y1),B(x2,y2),则M(4,y1),N(4,y2),且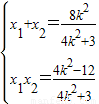 ,
,
∵直线AN方程是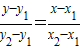 ,直线BM方程是
,直线BM方程是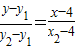 .
.
联立,得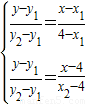 ,消去y,得:
,消去y,得: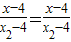 .
.
即(x1+x2-8)x=x1x2-16,即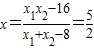 ,
,
把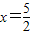 代入直线AN的方程
代入直线AN的方程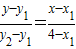 ,
,
得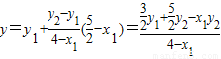 =
=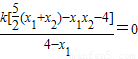 ,
,
∴AN与BM交于点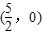 是x轴上一定点.
是x轴上一定点.
点评:本题考查直线与椭圆的位置关系、椭圆的方程及性质,考查学生的运算求解能力,难度较大.
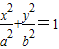 (a>b>0),由题意得
(a>b>0),由题意得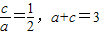 ,可得a,c,再由a2=b2+c2可得b;
,可得a,c,再由a2=b2+c2可得b;(2):①当AB垂直于x轴时,易证明;②当AB不垂直于x轴时,设直线AB的方程为y=k(x-1),代入椭圆
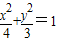 ,得(4k2+3)x2-8k2x+(4k2-12)=0,设A(x1,y1),B(x2,y2),写出直线AN、BM的方程联立,及韦达定理可求得AN与BM的交点,由其坐标可得结论;
,得(4k2+3)x2-8k2x+(4k2-12)=0,设A(x1,y1),B(x2,y2),写出直线AN、BM的方程联立,及韦达定理可求得AN与BM的交点,由其坐标可得结论;解答:(1)解:设椭圆C的方程为
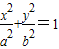 (a>b>0),
(a>b>0),则由
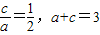 ,得a=2,c=1,b2=3,
,得a=2,c=1,b2=3,所以椭圆C的方程为
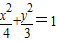 ;
;(2)证明:①当AB垂直于x轴时,AB的坐标分别为
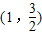 ,
,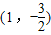 ,AN与BM的交点为
,AN与BM的交点为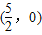 在x轴上.
在x轴上.②当AB不垂直于x轴时,设直线AB的方程为y=k(x-1),
代入椭圆
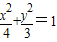 ,得(4k2+3)x2-8k2x+(4k2-12)=0,
,得(4k2+3)x2-8k2x+(4k2-12)=0,设A(x1,y1),B(x2,y2),则M(4,y1),N(4,y2),且
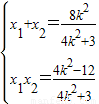 ,
,∵直线AN方程是
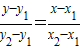 ,直线BM方程是
,直线BM方程是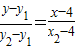 .
.联立,得
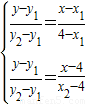 ,消去y,得:
,消去y,得: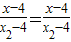 .
.即(x1+x2-8)x=x1x2-16,即
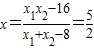 ,
,把
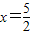 代入直线AN的方程
代入直线AN的方程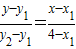 ,
,得
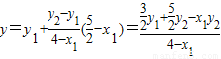 =
=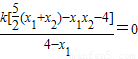 ,
,∴AN与BM交于点
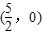 是x轴上一定点.
是x轴上一定点.点评:本题考查直线与椭圆的位置关系、椭圆的方程及性质,考查学生的运算求解能力,难度较大.

练习册系列答案
相关题目

 。
。