Question

如图，四棱锥P-ABCD的底面ABCD是菱形，∠BCD=60°，PA⊥面ABCD，E是AB的中点，F是PC的中点．
（Ⅰ）求证：面PDE⊥面PAB；
（Ⅱ）求证：BF∥面PDE．

Answer 1

分析：（I）证明DE⊥AB，DE⊥AP，利用线面垂直的判定定理，可得DE⊥面PAB，从而可证面PDE⊥面PAB；
（Ⅱ）证明FG与BE平行且相等，可得BF∥GE，利用线面平行的判定可得BF∥面．

解答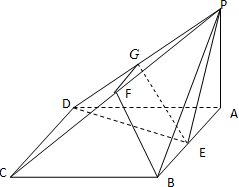：证明：（Ⅰ）∵底面ABCD是菱形，∠BCD=60°
∴△ABD为正三角形E是AB的中点，DE⊥AB-----------------------------------（2分）
∵PA⊥面ABCD，DE?面ABCD
∴DE⊥AP-----------------------------------（4分）
∵AB∩AP=A
∴DE⊥面PAB
∵DE?面PDE
∴面PDE⊥面PAB-----------------------------------（6分）
（Ⅱ）取PD的中点G，连结FG，GE，-----------------------------------（8分）
∵F，G是中点，∴FG∥CD且FG=

1

2

CD
∴FG与BE平行且相等，
∴BF∥GE-----------------------------------（10分）
∵GE?面PDE
∴BF∥面PDE．-----------------------------------（12分）

点评：本题考查线面垂直，面面垂直，考查线面平行，正确运用判定定理是关键．