题目内容
如图,已知正方形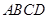 的边长为
的边长为 ,
, 在
在 延长线上,且
延长线上,且 .动点
.动点 从点
从点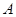 出发,沿正方形
出发,沿正方形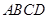 的边按逆时针方向运动一周回到
的边按逆时针方向运动一周回到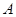 点,其中
点,其中 ,则下列命题正确的是 .(填上所有正确命题的序号)
,则下列命题正确的是 .(填上所有正确命题的序号)
① ;
;
②当点 为
为 中点时,
中点时, ;
;
③若 ,则点
,则点 有且只有一个;
有且只有一个;
④ 的最大值为
的最大值为 ;
;
⑤ 的最大值为
的最大值为 .
.
①②④⑤
解析试题分析:由题意,不妨设正方形的边长为1,建立如图所示的坐标系,
(1)则B(1,0),E(-1,1),故AB=(1,0),AE==(-1,1),所以
= ,由图像可知
,由图像可知 ,故①正确;
,故①正确;
(2)当点 为
为 中点时,
中点时,
 ,
, =
=  ,所以
,所以 =
= ,
,
解得 ,则
,则 ,故②正确;
,故②正确;
(3)当λ=1,μ=1时,AP=(1,1),此时点P与D重合,满足λ+μ=2,
当λ= ,μ=
,μ= 时,AP=(1,
时,AP=(1, ),此时点P为BC的中点,满足λ+μ=2,
),此时点P为BC的中点,满足λ+μ=2,
故满足λ+μ=2的点不唯一,故③错误;
(4)当P∈AB时,有0≤λ-μ≤1,μ=0,可得0≤λ≤1,故有0≤λ+μ≤1,
当P∈BC时,有λ-μ=1,0≤μ≤1,所以0≤λ-1≤1,故1≤λ≤2,故1≤λ+μ≤3,
当P∈CD时,有0≤λ-μ≤1,μ=1,所以0≤λ-1≤1,故1≤λ≤2,故2≤λ+μ≤3,
当P∈AD时,有λ-μ=0,0≤μ≤1,所以0≤λ≤1,故0≤λ+μ≤2,
综上可得0≤λ+μ≤3,故④正确,
(5) =
= =
=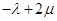 ,
,
当P∈AB时,有0≤λ-μ≤1,μ=0,可得0≤-λ≤1,故有-1≤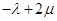 ≤0,
≤0,
当P∈BC时,有λ-μ=1,0≤μ≤1,0≤2μ≤2,所以0≤λ-1≤1,故1≤λ≤2,-2≤-λ≤-1
故-2≤-λ+2μ≤1,
当P∈CD时,有0≤λ-μ≤1,μ=1,所以0≤λ-1≤1,故1≤λ≤2,-2≤-λ≤-1,故-1≤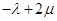 ≤0,
≤0,
当P∈AD时,有λ-μ=0,0≤μ≤1,所以0≤λ≤1,-1≤-λ≤0,故0≤-λ+2μ≤1,
综上可得-2≤-λ+2μ≤1,故⑤正确,
考点:向量加减的几何意义,向量的线性运算性质及几何意义

 阅读快车系列答案
阅读快车系列答案若 ,
, 且(
且( )⊥
)⊥ ,则
,则 与
与 的夹角是 ( )
的夹角是 ( )
A.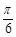 | B. | C. | D. |
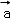 •
• =
= =
= ”;
”; •
• •
• 、
、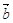 满足:
满足: ,
, ,
, ,则
,则 ________
________ ,则α和β的夹角θ的范围是 _________ .
,则α和β的夹角θ的范围是 _________ . ,
, (
( ),若
),若 ∥
∥ ,则
,则 =______________.
=______________. =
= ,且|
,且| |;
|; +
+ +
+ =0;
=0; =-5e1,且|
=-5e1,且| |,则四边形ABCD是等腰梯形;
|,则四边形ABCD是等腰梯形; |=5,则3≤|
|=5,则3≤| =
= =(1,1),
=(1,1), ·
· +
+ ·
· =
= ·
· ,则四边形ABCD的面积为________.
,则四边形ABCD的面积为________. =ma,
=ma,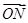 =nb,
=nb, =αa+βb,其中m,n,α,β均为实数,m≠0,n≠0,若M、P、N三点共线,则
=αa+βb,其中m,n,α,β均为实数,m≠0,n≠0,若M、P、N三点共线,则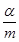 +
+ =________.
=________.