题目内容
在正三棱锥S-ABC中,SA=1,∠ASB=30°,过点A作三棱锥的截面AMN,求截面AMN周长的最小值为分析:本题考查的是三棱锥轴截面三角形周长最值问题.在解答时,首先采用侧面展开法将三棱锥的侧面展开结合题目信息分析知展开后图形是正方形的一部分,画图结合图形易知M、N、A与A′在一条线上时截面AMN的周长最小.进而问题即可获得解答.
解答: 解:由题意可知:将底面ABC去掉后展开平铺得一缺角正方形,
解:由题意可知:将底面ABC去掉后展开平铺得一缺角正方形,
将三棱锥中的A点分为正方形中的A点和A′点如图:
而AMN周长即为折线AMNA‘最小距离,
所以最小周长是:
.
故答案为:
.
 解:由题意可知:将底面ABC去掉后展开平铺得一缺角正方形,
解:由题意可知:将底面ABC去掉后展开平铺得一缺角正方形,将三棱锥中的A点分为正方形中的A点和A′点如图:
而AMN周长即为折线AMNA‘最小距离,
所以最小周长是:
| 2 |
故答案为:
| 2 |
点评:本题考查的是三棱锥轴截面三角形周长最值问题.在解答的过程当中充分体现了侧面展开的方法、两点之间直线最短的理论以及问题转化的能力.值得同学们体会反思.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
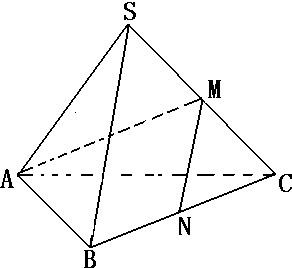 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|