题目内容
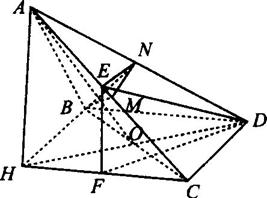
(21)如图,三定点![]()
![]()

(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
解法一:如图 (Ⅰ)设 D(xD,yD), E (xC,yC) , M (x,y).
由 ![]() =t
=t![]() =t
=t![]() ,知(xD-2,yD-1)=t(-2,-2).
,知(xD-2,yD-1)=t(-2,-2).
∴
![]() 同理
同理
∴kDC=![]() =
=![]() =1-2t.
=1-2t.
∵t∈[0,1], ∴kDC∈[-1,1].
(Ⅱ)∵![]() =t
=t![]() .
.
∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(-2t,4t2-2t).
∴![]() ∴y=
∴y=![]() ,即x2=4y.
,即x2=4y.
∵t∈[0,1],
∴x=2(1-2t)∈[-2,2].
即所求轨迹方程为 x2=4y , x∈[-2,2].

解法二:(Ⅰ)同上.
(Ⅱ)如图,
![]() ,
,
![]()
![]()
=(1-t)2![]()
设M点坐标为(x,y),由![]() 得
得
= 消去t得 x2=4y.
消去t得 x2=4y.
∵t∈[0,1],∴x∈[-2,2]. 故轨迹方程是 x2=4y, x∈[-2,2].

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目