Question

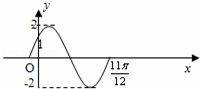
已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜）在一个周期内的图象如图所示．

（1）求函数的解析式；

（2）设0＜x＜π，且方程f（x）=m有两个不同的实数根，求实数m的取值范围和这两个根的和．

Answer 1

考点：

由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的定义域和值域．

专题：

计算题．

分析：

（1）通过函数的图象求出A，图象过（0，1）点，

求出ϕ，利用图象求出函数的周期，得到ω，即可求出函数的解析式；

（2）设0＜x＜π，且方程f（x）=m有两个不同的实数根，通过函数的图象结合函数的对称轴，直接求实数m的取值范围和这两个根的和．

解答：

解：（1）显然A=2，

又图象过（0，1）点，

∴f（0）=1，

∴，

∵，∴；

由图象结合“五点法”可知，对应函数y=sinx图象的点（2π，0），

∴，得ω=2．

所以所求的函数的解析式为：．

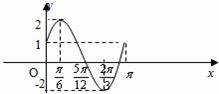
（2）如图所示，在同一坐标系中画出和y=m（m∈R）的图象，

由图可知，当﹣2＜m＜1或1＜m＜2时，直线y=m与曲线有两个不同的交点，即原方程有两个不同的实数根．

∴m的取值范围为：﹣2＜m＜1或1＜m＜2；

当﹣2＜m＜1时，两根和为；

当1＜m＜2时，两根和为．

点评：

本题是中档题，考查三角函数的解析式的求法，函数的图象的应用，考查计算能力，常考题型．