题目内容
（2013•临沂一模）已知向量
=（1，-2），
=（x，y），若x，y∈[1，4]，则满足
•
＞0的概率为
．
| a |
| b |
| a |
| b |
| 1 |
| 9 |
| 1 |
| 9 |
分析：先作出不等式组表示的平面区域
，然后求出表示的平面区域的面积，然后求出
•
＞0对应的区域的面积，代入几何概率的计算公式可求
|
| a |
| b |
解答：
解：∵
•
=x-2y
又∵
，其表示的平面区域为如图所示的矩形ABCD，面积为S=3×3=9
∴当
•
＞0时，有x-2y＞0，其对应的区域为如图所示的阴影部分的三角形区域，面积为S1=
×2×1=1
由几何概率的计算公式可得，所求的概率P=
故答案为：
解：∵| a |
| b |
又∵
|
∴当
| a |
| b |
| 1 |
| 2 |
由几何概率的计算公式可得，所求的概率P=
| 1 |
| 9 |
故答案为：
| 1 |
| 9 |
点评：本题主要考查了几何概率的求解公式的应用，解题的关键是准确求解出相应区域的面积
练习册系列答案
津桥教育计算小状元系列答案
相关题目
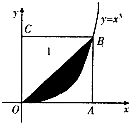（2013•临沂一模）如图所示，在边长为l的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（ ）
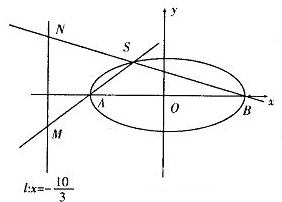（2013•临沂一模）如图，已知椭圆C：