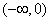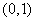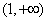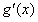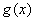题目内容
已知函数f(x)=x3-3x。
(1)求曲线y=f(x)在点x=2处的切线方程;
(2)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
(1)求曲线y=f(x)在点x=2处的切线方程;
(2)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
解:(1)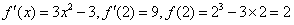 , ,∴曲线y=f(x)在x=2处的切线方程为 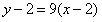 ,即9x-y-16=0。 ,即9x-y-16=0。(2)过点A(1,m)向曲线y=f(x)作切线,设切点为 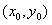 , ,则 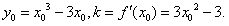 , ,则切线方程为 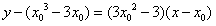 , ,将A(1,m)代入上式,整理得, 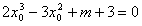 , ,∵过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线, ∴方程 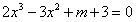 (*)有三个不同实数根, (*)有三个不同实数根,记 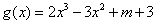 , ,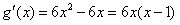 , ,令 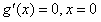 或1, 或1,则 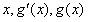 的变化情况如下表: 的变化情况如下表:
由题意有,当且仅当 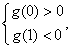 即 即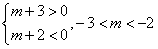 时,函数g(x)有三个不同零点, 时,函数g(x)有三个不同零点,此时过点A可作曲线y=f(x)的三条不同切线, 故m的范围是(-3,-2)。 |

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目