题目内容
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若PA=AB=BC=![]() AD.
AD.
(1)求证:CD⊥平面PAC;
(2)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置并证明,若不存在,请说明理由.
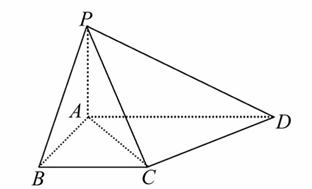
方法一:
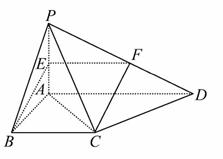 (1)因为∠PAD=90°,所以PA⊥AD.
(1)因为∠PAD=90°,所以PA⊥AD.
又因为侧面PAD⊥底面ABCD,且侧面PAD∩底面ABCD=AD,
所以PA⊥底面ABCD.
而CD⊂底面ABCD,
所以PA⊥CD.
在底面ABCD中,因为∠ABC=∠BAD=90°,AB=BC=![]() AD,
AD,
所以AC=CD=![]() AD,所以AC⊥CD.
AD,所以AC⊥CD.
又因为PA∩AC=A,所以CD⊥平面PAC.
(2)在PA上存在中点E,使得BE∥平面PCD,
证明如下:设PD的中点是F,
连结BE,EF,FC,
则EF∥AD,且EF=![]() AD.
AD.
由已知BC∥AD.又BC=![]() AD,
AD,
所以BC∥EF,且BC=EF,
所以四边形BEFC为平行四边形,所以BE∥CF.
因为BE![]() 平面PCD,CF⊂平面PCD,
平面PCD,CF⊂平面PCD,
所以BE∥平面PCD.
方法二:
因为∠PAD=90°,
所以PA⊥AD.
又因为侧面PAD⊥底面ABCD,
且侧面PAD∩底面ABCD=AD,
所以PA⊥底面ABCD.
又因为∠BAD=90°,
所以AB,AD,AP两两垂直.
分别以AB,AD,AP所在直线为x轴,y轴,z轴建立空间直角坐标系,如图
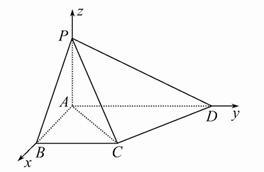
设AD=2,则A(0,0,0),B(1,0,0)![]() ,C(1,1,0),D(0,2,0),P(0,0,1).
,C(1,1,0),D(0,2,0),P(0,0,1).
(1)![]() =(0,0,1),
=(0,0,1),![]() =(1,1,0),
=(1,1,0),![]() =(-1,1,0),
=(-1,1,0),
所以![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,所以AP⊥CD,AC⊥CD.
=0,所以AP⊥CD,AC⊥CD.
又因为AP∩AC=A,所以CD⊥平面PAC.
(2)在PA上存在中点E,使得BE∥平面PCD,则E(0,0,![]() ),
),![]() =(-1,0,
=(-1,0,![]() ).设平面PCD的一个法向量是n=(x,y,z),则
).设平面PCD的一个法向量是n=(x,y,z),则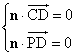 .
.
因为![]() =(-1,1,0),
=(-1,1,0),![]() =(0,2,-1),
=(0,2,-1),
所以![]() .取x=1,则n=(1,1,2).
.取x=1,则n=(1,1,2).
所以n·![]() =(1,1,2)·(-1,0,
=(1,1,2)·(-1,0,![]() )=0,
)=0,
所以n⊥![]() .
.
因为BE![]() 平面PCD,所以BE∥平面PCD.
平面PCD,所以BE∥平面PCD.

 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案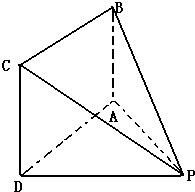 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且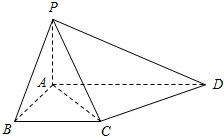 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=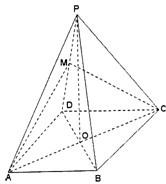 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.