Question

（2012•衡阳模拟）在长方形AA₁B₁B中，C，C₁分别是AB，A₁B₁的中点，且AB=2AA₁=4（如左图）将此长方形沿CC₁对折（如图），使平面AA₁C₁C⊥平面BB₁C₁C．

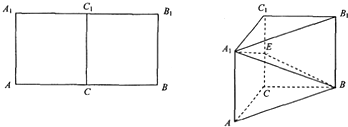
（1）求证：∠ACB=90°；
（2）当点E在棱CC₁上的什么位置时，平面BA₁E与平面AA₁C₁C所成的锐二面角为60°？

Answer 1

分析：（1）由AC⊥CC₁，BC⊥CC₁，得∠ACB是二面角A-CC₁-B的平面角，利用平面AA₁C₁C⊥平面BB₁C₁C，可证∠ACB=90°；
（2）建立直角坐标系，设E（0，0，t），求出平面BA₁E的法向量

n

=(

t-2

2

，

t

2

，1)，利用平面AA₁C₁C的法向量为

m

=（0，1，0），平面BA₁E与平面AA₁C₁C所成的锐二面角为60°，根据向量的夹角公式，即可求得结论．

解答：（1）证明：由AC⊥CC₁，BC⊥CC₁，得∠ACB是二面角A-CC₁-B的平面角
∵平面AA₁C₁C⊥平面BB₁C₁C．
∴∠ACB=90°；
（2）解：建立如图所示的直角坐标系，

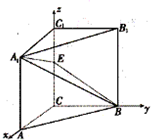
则A₁=（2，0，2），B（0，2，0），设E（0，0，t）
∴

A1E

=(-2，0，t-2)，

BE

=(0，-2，t)
设平面BA₁E的法向量为

n

=(x，y，z)，则

2x+(t-2)z=0 -2y+tz=0

令z=1，则

n

=(

t-2

2

，

t

2

，1)
∵平面AA₁C₁C的法向量为

m

=（0，1，0），平面BA₁E与平面AA₁C₁C所成的锐二面角为60°
∴cos60°=|

t 2

1× ( t-2 2 )2+ t2 4 +1

|，∴t=

5

-1
∴CE=

5

-1时，平面BA₁E与平面AA₁C₁C所成的锐二面角为60°．

点评：本题考查面面垂直，考查面面角，考查利用空间向量解决立体几何问题，属于中档题．