题目内容
已知 的展开式的二项式系数之和为32,则展开式中含
的展开式的二项式系数之和为32,则展开式中含 项的系数是( )
项的系数是( )
| A.5 | B.20 | C.10 | D.40 |
C
解析试题分析:先根据展开式的二项式系数之和求出n的值,然后利用二项式的展开式找出x的指数为1时r的值,从而可求出展开式中含x项的系数.解:根据题意,该二项式的展开式的二项式系数之和为32,则有2n=32,可得n=5,则二项式的展开式为Tr+1= x2(5-r)•x-r=
x2(5-r)•x-r= x10-3r,令10-3r=1解得r=3,∴展开式中含x项的系数是,
x10-3r,令10-3r=1解得r=3,∴展开式中含x项的系数是, =10,故选C.
=10,故选C.
考点:二项式定理
点评:本题主要考查二项式定理的应用,注意二项式的展开式的形式,要求准确记忆,同时考查了运算求解的能力,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有
| A.96种 | B.180种 | C.240种 | D.280种 |
已知二项式 的展开式中第四项为常数项,则
的展开式中第四项为常数项,则 等于
等于
| A.9 | B.6 | C.5 | D.3 |
设 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
| A.4 | B.5 | C.6 | D.8 |
某单位安排2013年春节期间7天假期的值班情况,7个员工每人各值一天. 已知某员工甲必须排在前两天,员工乙不能排在第一天,员工丙必须排在最后一天,则不同的值班顺序有( )
| A.120种 | B.216种 | C.720种 | D.540种 |
设(2 +
+ )
) =
= 则
则 值为 ( )
值为 ( )
| A.16 | B.-16 | C.1 | D.-1 |
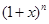 的展开式中,
的展开式中,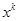 的系数可以表示从
的系数可以表示从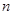 个不同物体中选出
个不同物体中选出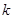 个的方法总数.下列各式的展开式中
个的方法总数.下列各式的展开式中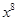 的系数恰能表示从重量分别为
的系数恰能表示从重量分别为 克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为
克的砝码(每种砝码各一个)中选出若干个,使其总重量恰为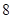 克的方法总数的选项是()
克的方法总数的选项是()
A.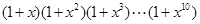 |
B. |
C.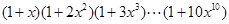 |
D.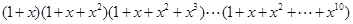 |
现进行医药下乡活动,某医院的4名男医生和4名女医生及2名护士要去两个不同的山区进行义诊,若每个山区去男、女医生各2名,并带1名护士,则不同的分配方法有( )
| A.144 | B.72 | C.36 | D.16 |
在 的展开式中,
的展开式中, 的系数为( )
的系数为( )
A. | B. | C. | D. |