题目内容
(本题满分12分)已知函数
在R上是减函数，求实数
的取值范围。
a 
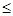-3。
解析试题分析：f′(x)= 
，由已知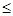0在R上恒成立。
当a=0时，6x-1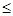0，得x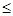
，在R上不恒成立。
当a
0时，要使得f′(x) 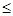0在R上恒成立，须满足a<0且△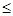0，
解得a 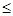-3，故当a 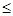-3时，函数
在R上是减函数.
考点：利用导数研究函数的单调性。
点评：若
恒成立
；若
恒成立
。此题中没有限制二次项系数不为零，所以不要忘记讨论。
练习册系列答案
相关题目
的三个内角
、
、
所对的边分别为
、
、
.
，且
.（1）求
.求
.
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
：
的长轴长是短轴长的
倍，
，
是它的左，右焦点．
，且
，
，求
作以
（
是切点），且使
，求动点
的长轴，短轴端点分别是A,B，从椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点，向量
与
是共线向量
分别是左右焦点，求
的取值范围