题目内容
本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知a为实数,f(x)=a-
(x∈R).
(1)求证:对于任意实数a,y=f(x)在(-∞,+∞)上是增函数;
(2)当f(x)是奇函数时,若方程f-1(x)=log2(x+t)总有实数根,求实数t的取值范围.
已知a为实数,f(x)=a-
| 2 |
| 2x+1 |
(1)求证:对于任意实数a,y=f(x)在(-∞,+∞)上是增函数;
(2)当f(x)是奇函数时,若方程f-1(x)=log2(x+t)总有实数根,求实数t的取值范围.
(1)∵f(x)=a-
(x∈R)
∴f(x)的导数为f'(x)=-
=
>0在(-∞,+∞)上恒成立
∴对于任意实数a,y=f(x)在(-∞,+∞)上是增函数;
(2)因为f(x)是R上的奇函数,所以f(0)=a-
=0,可得a=1.
∴f(x)=1-
=
,
令y=
,可得2x=
,x=log2
,(-1<y<1)
∴函数f(x)的反函数为:f-1(x)=log2
(-1<x<1)
由log2
=log2(x+t)得
=x+t,即-1+
=x+t,
∴t=(1-x)+
-2≥2
-2
当且仅当1-x=
,即x=1-
时等号成立,
所以,t的取值范围是[2
-2,+∞).
| 2 |
| 2x+1 |
∴f(x)的导数为f'(x)=-
| -2×2xln2 |
| (2x+1)2 |
| 2x+1ln2 |
| (2x+1)2 |
∴对于任意实数a,y=f(x)在(-∞,+∞)上是增函数;
(2)因为f(x)是R上的奇函数,所以f(0)=a-
| 2 |
| 20+1 |
∴f(x)=1-
| 2 |
| 2x+1 |
| 1-2x |
| 2x+1 |
令y=
| 1-2x |
| 2x+1 |
| 1+y |
| 1-y |
| 1+y |
| 1-y |
∴函数f(x)的反函数为:f-1(x)=log2
| 1+x |
| 1-x |
由log2
| 1+x |
| 1-x |
| 1+x |
| 1-x |
| 2 |
| 1-x |
∴t=(1-x)+
| 2 |
| 1-x |
| 2 |
当且仅当1-x=
| 2 |
| 1-x |
| 2 |
所以,t的取值范围是[2
| 2 |

练习册系列答案
相关题目
 (2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分
(2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分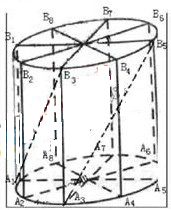 (1)当圆柱底面半径
(1)当圆柱底面半径 且与向量
且与向量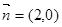 夹角为
夹角为 ,其中A,B,C是
,其中A,B,C是 的内角。
的内角。 的取值范围。
的取值范围。