题目内容
已知数列{an}前n项和为Sn,且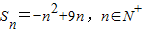 .
.(1)求{an}的通项;
(2)设Tn=|a1|+|a2|+…|an|,求Tn.
【答案】分析:(1)①当n=1时,a1=S1=8,②当n≥2时,an=Sn-Sn-1=-2n+10,检验可得an=-2n+10;(2)可知数列的前5项≤0,从第6项开始全为负值,分类讨论可得.
解答:解:(1)①当n=1时,a1=S1=8…(2分)
②当n≥2时,an=Sn-Sn-1
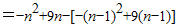
=-2n+10
检验:a1适合an=-2n+10…(5分)
综合①②得:an=-2n+10…(6分)
(2)①当n≤5时,Tn=|a1|+|a2|+…|an|=a1+a2+a3+…+an=-n2+9n…(8分)
②当n≥6时,Tn=|a1|+|a2|+…|an|=(a1+a2+…+a5)-(a6+a7+…+an)
=2(a1+a2+…+a5)-(a1+a2+…+an)=n2-9n+40…(11分)
综合①②得: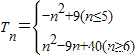 …(12分)
…(12分)
点评:本题考查数列的求和,以及由数列的前n项和求其通项,涉及分类讨论的思想,属中档题.
解答:解:(1)①当n=1时,a1=S1=8…(2分)
②当n≥2时,an=Sn-Sn-1
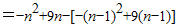
=-2n+10
检验:a1适合an=-2n+10…(5分)
综合①②得:an=-2n+10…(6分)
(2)①当n≤5时,Tn=|a1|+|a2|+…|an|=a1+a2+a3+…+an=-n2+9n…(8分)
②当n≥6时,Tn=|a1|+|a2|+…|an|=(a1+a2+…+a5)-(a6+a7+…+an)
=2(a1+a2+…+a5)-(a1+a2+…+an)=n2-9n+40…(11分)
综合①②得:
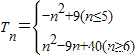 …(12分)
…(12分)点评:本题考查数列的求和,以及由数列的前n项和求其通项,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目