题目内容
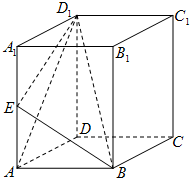 如图,ABCD-A1B1C1D1是四棱柱,底面ABCD是菱形,AA1⊥底面ABCD,AB=2,∠BAD=60°,E是AA1的中点.
如图,ABCD-A1B1C1D1是四棱柱,底面ABCD是菱形,AA1⊥底面ABCD,AB=2,∠BAD=60°,E是AA1的中点.(1)求证:平面BD1E⊥平面BB1D1D;
(2)若四面体D1-ABE的体积V=1,求棱柱ABCD-A1B1C1D1的高.
分析:(1)设平面BD1E∩CC1=F,连接BF,由已知中ABCD-A1B1C1D1是四棱柱,底面ABCD是菱形,AA1⊥底面ABCD,我们结合直四棱柱的几何特征得到△D1A1E≌△BCF,连接A1C1、B1D1,可以得到AA1⊥A1C1,A1C1⊥BB1,进而由线面垂直的判定定理得到EF⊥平面BB1D1D,再由线面垂直的性质,可得平面BD1E⊥平面BB1D1D;
(2)因为AA1⊥底面ABCD,所以AA1是棱柱ABCD-A1B1C1D1的高,我们求出三角形ABE的面积,结合四面体D1-ABE的体积V=1,我们易求出AA1的值,即棱柱ABCD-A1B1C1D1的高.
(2)因为AA1⊥底面ABCD,所以AA1是棱柱ABCD-A1B1C1D1的高,我们求出三角形ABE的面积,结合四面体D1-ABE的体积V=1,我们易求出AA1的值,即棱柱ABCD-A1B1C1D1的高.
解答:解:(1)设平面BD1E∩CC1=F,连接BF,则△D1A1E与△BCF的对应边互相平行(1分),
且A1D1=BC,所以△D1A1E≌△BCF(2分),
F是CC1的中点(3分),
连接A1C1、B1D1,因为AA1⊥底面ABCD,所以AA1⊥A1C1,A1C1⊥BB1(4分),
ABCD是菱形,A1C1⊥B1D1,且BB1∩B1D1=B1,所以A1C1⊥面BB1D1D(5分),
因为E、F分别是AA1、CC1的中点,所以A1EFC1是矩形,EF∥A1C1,所以EF⊥平面BB1D1D(6分),
EF?平面BD1E(即平面BFD1E),所以,面BD1E⊥面BB1D1D(7分).
(2)因为AA1⊥底面ABCD,所以AA1是棱柱ABCD-A1B1C1D1的高(8分),
AA1?平面ABB1A1,平面ABB1A1⊥底面ABCD(9分),
在底面A1B1C1D1上作D1F⊥A1B1,垂足为F,面ABB1A1∩面A1B1C1D1=A1B1,所以D1F⊥面ABB1A1(10分),
所以V=
×S△ABE×D1F(11分),
其中S△ABE=
×AE×AB=AE=
AA1,D1F=A1D1×sin60o=
(12分),
所以V=
×
AA 1×
=1(13分),
解得AA 1=2
,即棱柱ABCD-A1B1C1D1的高为2
(14分).
且A1D1=BC,所以△D1A1E≌△BCF(2分),
F是CC1的中点(3分),
连接A1C1、B1D1,因为AA1⊥底面ABCD,所以AA1⊥A1C1,A1C1⊥BB1(4分),
ABCD是菱形,A1C1⊥B1D1,且BB1∩B1D1=B1,所以A1C1⊥面BB1D1D(5分),
因为E、F分别是AA1、CC1的中点,所以A1EFC1是矩形,EF∥A1C1,所以EF⊥平面BB1D1D(6分),
EF?平面BD1E(即平面BFD1E),所以,面BD1E⊥面BB1D1D(7分).
(2)因为AA1⊥底面ABCD,所以AA1是棱柱ABCD-A1B1C1D1的高(8分),
AA1?平面ABB1A1,平面ABB1A1⊥底面ABCD(9分),
在底面A1B1C1D1上作D1F⊥A1B1,垂足为F,面ABB1A1∩面A1B1C1D1=A1B1,所以D1F⊥面ABB1A1(10分),
所以V=
| 1 |
| 3 |
其中S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
所以V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
解得AA 1=2
| 3 |
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,熟练掌握棱柱的几何特征,结合已知条件找出证明线面垂直及面面垂直的条件是解答本题的关键.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
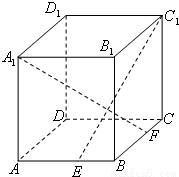
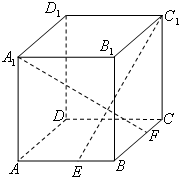 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是