题目内容
已知a>0,b>0,不等式 的解集是________.
的解集是________.

分析:在a>0,b>0的条件下将-b<
 <a转化为
<a转化为 即可求得答案.
即可求得答案.解答:∵-b<
 <a,
<a,∴
 +b>0且
+b>0且 -a<0,
-a<0,∵b>0,由
 >0,解得x>0或x<-
>0,解得x>0或x<- ;①
;① -a<0,得
-a<0,得 <0?
<0?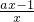 >0,∵a>0,
>0,∵a>0,∴x>
 或x<0;②
或x<0;②由①②得:x>
 或x<-
或x<- ;
;∴不等式-b<
 <a的解集是(-∞,-
<a的解集是(-∞,- )∪(
)∪( ,+∞).
,+∞).故答案为:(-∞,-
 )∪(
)∪( ,+∞).
,+∞).点评:本题考查分式不等式组的解法,将-b<
 <a转化为
<a转化为 是关键,也是难点,考查化归思想与分析运算的能力,属于中档题.
是关键,也是难点,考查化归思想与分析运算的能力,属于中档题. 
练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目