题目内容
已知直三棱柱ABC-A1B1C1中,D,E分别为AA1,CC1的中点,AC⊥BC,点F在线段AB上,且AB=4AF.
(Ⅰ)求证:BC⊥C1D;
(Ⅱ)若M为线段BE上一点,BE=4ME求证:C1D∥平面B1FM.
(Ⅰ)求证:BC⊥C1D;
(Ⅱ)若M为线段BE上一点,BE=4ME求证:C1D∥平面B1FM.


(Ⅰ)由直三棱柱可知CC1⊥平面ABC,所以CC1⊥AC,…(2分)
又因为AC⊥BF,CC1∩BF=F,AC⊥面BCF,
故AC⊥BC,…(4分)
又在直三棱柱中,CC1⊥BC,CC1∩AC=C,
故BC⊥面AC1C,C1D在平面ACC1内,所以BC⊥C1D; …(6分)
(Ⅱ)连结FM,B1M,FB1在△BEA中,由BE=4ME,AB=4AF,所以MF∥AE,
又在面AA1C1C中,易证C1D∥AE,所以C1D∥平面B1FM. …(14分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.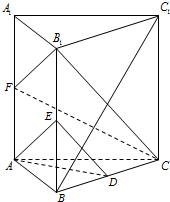 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.