题目内容
如图,AB是⊙O的直径,C是⊙O外一点,且AC=AB,BC交⊙O于点D.已知BC=4,AD=6,AC交⊙O于点E,求四边形ABDE的周长.
【答案】分析:由题意,可由AB是⊙O的直径及AC=AB得出D是中点,由此求得BD,BC的值,再∠DEC=∠B得出∠DEC=∠C,即可求出DE,由图形可得出CE•CA=CD•CB,由此方程解出AE,再求周长即可
解答: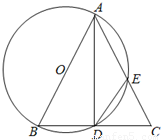 解:因为AB是⊙O的直径,所以AD⊥BC,所以AD
解:因为AB是⊙O的直径,所以AD⊥BC,所以AD
是△ABC的中线,所以AB=AC=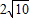 ,BD=DC=2. …(4分)
,BD=DC=2. …(4分)
由∠DEC=∠B=∠C,所以DE=DC=2.…(6分)
由CE•CA=CD•CB,得CE=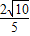 ,所以
,所以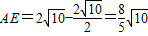 .…(8分)
.…(8分)
所以四边形ABDE的周长为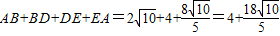 . …(10分)
. …(10分)
点评:本题考点是与圆有关的比例线段,考察了弦切角定理,切割线定理等,解题的关键是能根据圆中的相关定理建立方程解出相关的量,是与圆有关的基本题
解答:
 解:因为AB是⊙O的直径,所以AD⊥BC,所以AD
解:因为AB是⊙O的直径,所以AD⊥BC,所以AD是△ABC的中线,所以AB=AC=
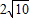 ,BD=DC=2. …(4分)
,BD=DC=2. …(4分)由∠DEC=∠B=∠C,所以DE=DC=2.…(6分)
由CE•CA=CD•CB,得CE=
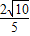 ,所以
,所以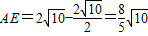 .…(8分)
.…(8分)所以四边形ABDE的周长为
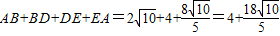 . …(10分)
. …(10分)点评:本题考点是与圆有关的比例线段,考察了弦切角定理,切割线定理等,解题的关键是能根据圆中的相关定理建立方程解出相关的量,是与圆有关的基本题

练习册系列答案
相关题目






 面体中有
面体中有 个面是直角三角形,则称这个
个面是直角三角形,则称这个 .那么四面体
.那么四面体 的直度为多少?说明理由;
的直度为多少?说明理由; (2)在四面体
(2)在四面体 ,设
,设 .若动点
.若动点 在四面体
在四面体 .设
.设 为动点
为动点 的函数,求
的函数,求 的正切值.
的正切值.