题目内容
已知椭圆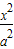 +
+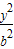 =1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线x-y+b=0是抛物线y2=4x的一条切线.
=1(a>b>0)的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线x-y+b=0是抛物线y2=4x的一条切线.(Ⅰ)求椭圆的方程;
(Ⅱ)过点S(0,
 )的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求点T坐标;若不存在,说明理由.
)的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求点T坐标;若不存在,说明理由.
【答案】分析:(Ⅰ)由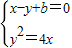 消去y,得:x2+(2b-4)x+b2=0,因直线y=x+b与抛物线y2=4x相切,b=1.圆
消去y,得:x2+(2b-4)x+b2=0,因直线y=x+b与抛物线y2=4x相切,b=1.圆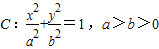 的两焦点与短轴的一个端点的连线构成等腰直角三角形,由此能求出椭圆方程.
的两焦点与短轴的一个端点的连线构成等腰直角三角形,由此能求出椭圆方程.
(Ⅱ)当L与x轴平行时,以AB为直径的圆的方程: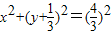 ,当L与x轴垂直时,以AB为直径的圆的方程:x2+y2=1.由
,当L与x轴垂直时,以AB为直径的圆的方程:x2+y2=1.由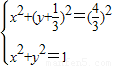 ,解得两圆公共点(0,1).因此所求的点T如果存在,只能是(0,1).由此能够导出以AB为直径的圆恒过点T(0,1).
,解得两圆公共点(0,1).因此所求的点T如果存在,只能是(0,1).由此能够导出以AB为直径的圆恒过点T(0,1).
解答:解:(Ⅰ)由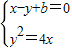 消去y,得:x2+(2b-4)x+b2=0,
消去y,得:x2+(2b-4)x+b2=0,
因直线y=x+b与抛物线y2=4x相切,∴△=(2b-4)2-4b2,∴b=1.…(2分)
∵圆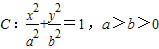 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
∴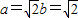 ,…(4分)
,…(4分)
故所求椭圆方程为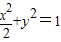 .…(5分)
.…(5分)
(Ⅱ)当L与x轴平行时,以AB为直径的圆的方程: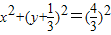 ,
,
当L与x轴垂直时,以AB为直径的圆的方程:x2+y2=1
由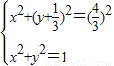
解得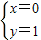 ,
,
即两圆公共点(0,1)因此,所求的点T如果存在,只能是(0,1)…(7分)
(ⅰ)当直线L斜率不存在时,以AB为直径的圆过点T(0,1)
(ⅱ)若直线L斜率存在时,可设直线L:y=kx- .
.
由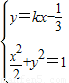 ,消去y得:(18k2+9)x2-12kx-16=0,
,消去y得:(18k2+9)x2-12kx-16=0,
记点A(x1,y1)、B(x2,y2),则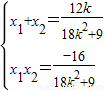 ,…(9分)
,…(9分)
∵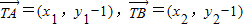 ,
,
∴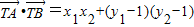
=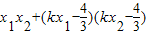
=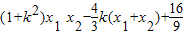
=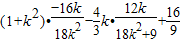
=0.
∴TA⊥TB,…(11分)
综合(ⅰ)(ⅱ),以AB为直径的圆恒过点T(0,1). …(12分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
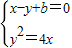 消去y,得:x2+(2b-4)x+b2=0,因直线y=x+b与抛物线y2=4x相切,b=1.圆
消去y,得:x2+(2b-4)x+b2=0,因直线y=x+b与抛物线y2=4x相切,b=1.圆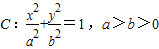 的两焦点与短轴的一个端点的连线构成等腰直角三角形,由此能求出椭圆方程.
的两焦点与短轴的一个端点的连线构成等腰直角三角形,由此能求出椭圆方程.(Ⅱ)当L与x轴平行时,以AB为直径的圆的方程:
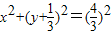 ,当L与x轴垂直时,以AB为直径的圆的方程:x2+y2=1.由
,当L与x轴垂直时,以AB为直径的圆的方程:x2+y2=1.由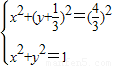 ,解得两圆公共点(0,1).因此所求的点T如果存在,只能是(0,1).由此能够导出以AB为直径的圆恒过点T(0,1).
,解得两圆公共点(0,1).因此所求的点T如果存在,只能是(0,1).由此能够导出以AB为直径的圆恒过点T(0,1).解答:解:(Ⅰ)由
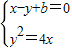 消去y,得:x2+(2b-4)x+b2=0,
消去y,得:x2+(2b-4)x+b2=0,因直线y=x+b与抛物线y2=4x相切,∴△=(2b-4)2-4b2,∴b=1.…(2分)
∵圆
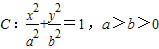 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,∴
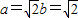 ,…(4分)
,…(4分)故所求椭圆方程为
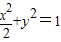 .…(5分)
.…(5分)(Ⅱ)当L与x轴平行时,以AB为直径的圆的方程:
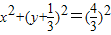 ,
,当L与x轴垂直时,以AB为直径的圆的方程:x2+y2=1
由
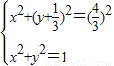
解得
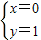 ,
,即两圆公共点(0,1)因此,所求的点T如果存在,只能是(0,1)…(7分)
(ⅰ)当直线L斜率不存在时,以AB为直径的圆过点T(0,1)
(ⅱ)若直线L斜率存在时,可设直线L:y=kx-
 .
.由
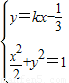 ,消去y得:(18k2+9)x2-12kx-16=0,
,消去y得:(18k2+9)x2-12kx-16=0,记点A(x1,y1)、B(x2,y2),则
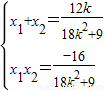 ,…(9分)
,…(9分)∵
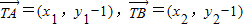 ,
,∴
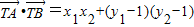
=
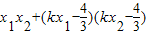
=
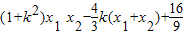
=
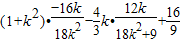
=0.
∴TA⊥TB,…(11分)
综合(ⅰ)(ⅱ),以AB为直径的圆恒过点T(0,1). …(12分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 ,则椭圆方程为( )
,则椭圆方程为( ) +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则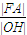 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为 B、
B、 C、
C、 D、
D、