题目内容

求满足下面条件的x的集合tan(2x-)+3＞0.

思路分析：本题可将2x-看作一个整体，利用y=tanx的图象及单调性求解.

解：原不等式可化为tan（2x-）＞，

设z=2x-.

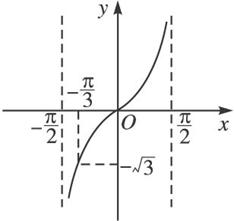
如下图，在（-，）上满足tanz＞的角的范围是-＜z＜,所以在整个定义域上有-+kπ＜z＜+kπ,k∈Z,

即-+kπ＜2x-＜+kπ,k∈Z.

解得＜x＜+,k∈Z.

所以原不等式的解集是

{x|＜x＜+,k∈Z}.

温馨提示

    本题是运用整体换元思想与数形结合思想解决的.首先将2x-看作一个变量Z，然后结合正切函数的图象得到Z的范围，最后用2x-替换Z，解得x即可.

练习册系列答案
相关题目
设函数y=f（x）是定义在R上的函数，并且满足下面三个条件；
①对任意正数x，y，都有f（xy）=f（x）+f（y）；
②当x＞1时，f（x）＜0；
③f（3）=-1．
（Ⅰ）求f(1)，f(
19
)的值；
（Ⅱ）证明f（x）在R+是减函数；
（Ⅲ）如果不等式f（x）+f（2-x）＜2成立，求x的取值范围．
设函数y=f（x）是定义在R+上的函数，并且满足下面三个条件：①对任意正数x，y 都有f（xy）=f（x）+f（y）；②当x＞1时，f（x）＜0；③f（3）=-1．
（1）求f（1），f（
19
）的值；
（2）证明：f（x）在R+上是减函数；
（3）如果不等式分f（x）+f（2-x）＜2成立，求x的取值范围．
将一枚质地均匀且四个面上分别标有1，2，3，4的正四面体先后抛掷两次，其底面落于桌面上，记第一次朝下面的数字为x，第二次朝下面的数字为y
（1）求满足条件“
xy
为整数”的事件的概率；
（2）求满足条件“x-y＜2”的事件的概率．
函数f（x）满足：（1）定义域是（0，+∞）；
（2）当x＞1时，f（x）＜2；
（3）对任意x，y∈（0，+∞），总有f（xy）=f（x）+f（y）-2．
回答下面的问题
（1）求出f（1）的值；
（2）写出一个满足上述条件的具体函数；
（3）判断函数f（x）的单调性，并用单调性的定义证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网