Question

【题目】在直棱柱中，已知，设中点为，中点为．

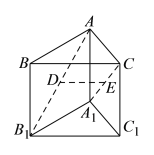
（Ⅰ）求证：平面．

（Ⅱ）求证：平面平面．

Answer 1

【答案】(1)见解析；（2）见解析.

【解析】分析：（Ⅰ）要证平面，只需在平面内找一条直线与直线平行。连结，在矩形中，由是的中点，可得是的中点，再由是的中点，可得，由直线与平面平行的判定定理可得平面。（Ⅱ）要证两个平面垂直，应在一个平面内找一条直线与另一个平面垂直。由是直棱柱，可得侧棱平面，进而得。因为，由直线与平面垂直的判定定理可得平面，进而由平面与平面垂直的判定定理，可得平面平面。

详解：（Ⅰ）证明：连结，

∵是的中点，

∴是的中点，

∵在中，是的中点，是的中点，

∴，

又平面，平面，

∴平面．

（Ⅱ）证明：∵是直棱柱，

∴平面，

∴，

又，

∴平面，

∵平面，

∴平面平面．