题目内容
已知一个等差数列的前四项之和为21,末四项之和为67,前n项和为286,则项数n为
- A.24
- B.26
- C.27
- D.28
B
分析:由等差数列的定义和性质可得首项与末项之和等于 =22,再由前n项和为286=
=22,再由前n项和为286=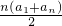 =11n,求得
=11n,求得
n的值.
解答:由等差数列的定义和性质可得首项与末项之和等于 =22,
=22,
再由前n项和为286=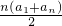 =11n,n=26,
=11n,n=26,
故选B.
点评:本题主要考查等差数列的定义和性质,前n项和公式的应用,求得首项与末项之和等于 =22,是解题的关键,属于基础题.
=22,是解题的关键,属于基础题.
分析:由等差数列的定义和性质可得首项与末项之和等于
 =22,再由前n项和为286=
=22,再由前n项和为286=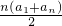 =11n,求得
=11n,求得n的值.
解答:由等差数列的定义和性质可得首项与末项之和等于
 =22,
=22,再由前n项和为286=
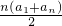 =11n,n=26,
=11n,n=26,故选B.
点评:本题主要考查等差数列的定义和性质,前n项和公式的应用,求得首项与末项之和等于
 =22,是解题的关键,属于基础题.
=22,是解题的关键,属于基础题. 
练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目