题目内容
设变量x，y满足约束条件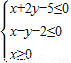
，则目标函数z=2x+3y+1的最大值为（ ）A．11
B．10
C．9
D．8.5
【答案】分析：首先做出可行域，将目标函数转化为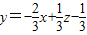
，求z的最大值，只需求直线l：
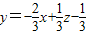在y轴上截距最大即可．
解答：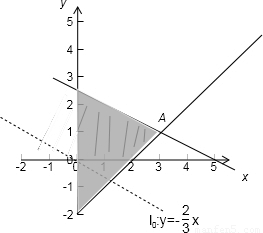
解：做出可行域如图所示：
将目标函数转化为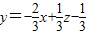
，
欲求z的最大值，
只需求直线l：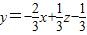
在y轴上的截距的最大值即可．
作出直线l：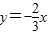
，将直线l平行移动，得到一系列的平行直线当直线经过点A时在y轴上的截距最大，此时z最大．
由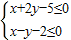
可求得A（3，1），
将A点坐标代入z=2x+3y+1解得z的最大值为2×3+3×1+1=10
故选B
点评：本题考查线性规划问题，考查数形集合思想解题，属基本题型的考查．
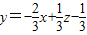，求z的最大值，只需求直线l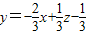：在y轴上截距最大即可．解答：
解：做出可行域如图所示：将目标函数转化为
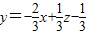，欲求z的最大值，
只需求直线l：
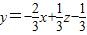在y轴上的截距的最大值即可．作出直线l：
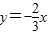，将直线l平行移动，得到一系列的平行直线当直线经过点A时在y轴上的截距最大，此时z最大．由
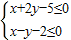可求得A（3，1），将A点坐标代入z=2x+3y+1解得z的最大值为2×3+3×1+1=10
故选B
点评：本题考查线性规划问题，考查数形集合思想解题，属基本题型的考查．
练习册系列答案
相关题目
设变量x，y满足约束条件
，则目标函数u=x2+y2的最大值M与最小值N的比
=（ ）
|
| M |
| N |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|