题目内容
已知椭圆 +
+ =1(a>b>0),半焦距为c(c>0),且满足(2a-3c)+(a-c)i=i(其中i为虚数单位),经过椭圆的左焦点F(-c,0),斜率为k1(k1≠0)的直线与椭圆交于A,B两点,O为坐标原点.
=1(a>b>0),半焦距为c(c>0),且满足(2a-3c)+(a-c)i=i(其中i为虚数单位),经过椭圆的左焦点F(-c,0),斜率为k1(k1≠0)的直线与椭圆交于A,B两点,O为坐标原点.
(1)求椭圆的标准方程;
(2)当k1=1时,求S△AOB的值;
(3)设R(1,0),延长AR,BR分别与椭圆交于C,D两点,直线CD的斜率为k2,求证: 为定值.
为定值.
(1)解:∵(2a-3c)+(a-c)i=i,∴2a-3c=0且a-c=1,∴a=3,c=2
∴b2=a2-c2=5,
故椭圆的方程为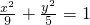 ;
;
(2)解:由(1)知F(-2,0),∴直线AB的方程为y=x+2,
代入椭圆方程,消去y可得14x2+36x-9=0.
设A(x1,y1),B(x2,y2),则x1+x2=-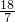 ,x1x2=-
,x1x2=-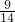
∴|AB|= |x1-x2|=
|x1-x2|=
设O点到直线AB的距离为d,则d= =
=
∴S△AOB= |AB|•d=
|AB|•d= ×
× ×
× =
= ;
;
(3)证明:设C(x3,y3),D(x4,y4),
由已知,直线AR的方程为y= ,即
,即
代入椭圆方程消去x并整理,得
则y1y3=- ,∴y3=
,∴y3=
∴ =
=
∴C( )
)
同理D( )
)
∴k2= =
=
∵y1=k1(x1+2),y2=k2(x2+2),
∴k2= =
= =
=
∴ =
=
分析:(1)根据(2a-3c)+(a-c)i=i,可求a,c的值,利用b2=a2-c2=5,即可求椭圆Γ的方程;
(2)设直线AB的方程为y=x+2,代入椭圆方程,消去y可得14x2+36x-9=0,求出|AB|,O点到直线AB的距离为d,即可求S△AOB的值;
(3)求出直线AR的方程,代入椭圆方程消去x并整理,从而可得C的坐标,同理可得D的坐标,进而可求斜率,化简,即可得到结论.
点评:本题考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识,考查运算求解能力,推理论证能力,属于中档题.
∴b2=a2-c2=5,
故椭圆的方程为
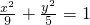 ;
;(2)解:由(1)知F(-2,0),∴直线AB的方程为y=x+2,
代入椭圆方程,消去y可得14x2+36x-9=0.
设A(x1,y1),B(x2,y2),则x1+x2=-
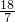 ,x1x2=-
,x1x2=-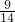
∴|AB|=
 |x1-x2|=
|x1-x2|=
设O点到直线AB的距离为d,则d=
 =
=
∴S△AOB=
 |AB|•d=
|AB|•d= ×
× ×
× =
= ;
;(3)证明:设C(x3,y3),D(x4,y4),
由已知,直线AR的方程为y=
 ,即
,即
代入椭圆方程消去x并整理,得

则y1y3=-
 ,∴y3=
,∴y3=
∴
 =
=
∴C(
 )
)同理D(
 )
)∴k2=
 =
=
∵y1=k1(x1+2),y2=k2(x2+2),
∴k2=
 =
= =
=
∴
 =
=
分析:(1)根据(2a-3c)+(a-c)i=i,可求a,c的值,利用b2=a2-c2=5,即可求椭圆Γ的方程;
(2)设直线AB的方程为y=x+2,代入椭圆方程,消去y可得14x2+36x-9=0,求出|AB|,O点到直线AB的距离为d,即可求S△AOB的值;
(3)求出直线AR的方程,代入椭圆方程消去x并整理,从而可得C的坐标,同理可得D的坐标,进而可求斜率,化简,即可得到结论.
点评:本题考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识,考查运算求解能力,推理论证能力,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 ,则椭圆方程为( )
,则椭圆方程为( ) +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则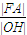 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为 B、
B、 C、
C、 D、
D、