题目内容
设三次函数![]() 在
在![]() 处取得极值,其图象在
处取得极值,其图象在![]() 处的切线的斜率为
处的切线的斜率为![]() 。求证:
。求证:![]() ;
;
略
解析:
(Ⅰ)方法一、![]() .由题设,得
.由题设,得![]() ①
①
![]() ②
②
∵![]() ,∴
,∴![]() ,∴
,∴![]() 。
。
由①代入②得![]() ,∴
,∴![]() ,
,
得![]() ∴
∴![]() 或
或![]() ③
③
将![]() 代入
代入![]() 中,得
中,得![]() ④
④
由③、④得![]() ;
;
方法二、同上可得:![]() 将(1)变为:
将(1)变为:![]() 代入(2)可得:
代入(2)可得: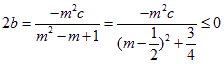 ,所以
,所以![]() ,则
,则![]()
方法三:同上可得:![]() 将(1)变为:
将(1)变为:![]() 代入(2)可得:
代入(2)可得:![]() ,显然
,显然![]() ,所以
,所以![]()
因为![]() 图象的开口向下,且有一根为x1=1
图象的开口向下,且有一根为x1=1
由韦达定理得![]() ,
,![]()
![]() ,所以
,所以![]() ,即
,即![]() ,则
,则![]() ,由
,由![]() 得:
得:![]()
所以:![]()

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
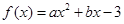 在
在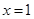 处取得极值,且在
处取得极值,且在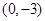 点处的切线与直线
点处的切线与直线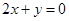 平行.
平行. 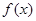 的解析式; (2)求函数
的解析式; (2)求函数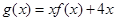 的单调递增区间及极值;
的单调递增区间及极值;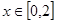 的最值.
的最值.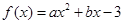 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行。
平行。  的解析式;
的解析式;  的单调递增区间及极值;
的单调递增区间及极值; 的最值。
的最值。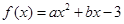 在
在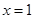 处取得极值,且在
处取得极值,且在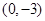 点处的切线与直线
点处的切线与直线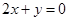 平行.
平行.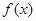 的解析式;
的解析式;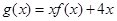 的单调递增区间与极值.
的单调递增区间与极值.