ЬтФПФкШн
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЌЁЪЧЧњЯп ЩЯЕФЕуЃЌA1ЃЈa1ЃЌ0ЃЉЃЌA2ЃЈa2ЃЌ0ЃЉЃЌЁЃЌAnЃЈanЃЌ0ЃЉЃЌЁЪЧxжсе§АыжсЩЯЕФЕуЃЌЧвЁїAA1P1ЃЌЁїA1A2P2ЃЌЁЃЌЁїAn-1AnPnЃЌЁОљЮЊаББпдкxжсЩЯЕФЕШбќжБНЧШ§НЧаЮЃЈAЮЊзјБъдЕуЃЉЃЎ
ЩЯЕФЕуЃЌA1ЃЈa1ЃЌ0ЃЉЃЌA2ЃЈa2ЃЌ0ЃЉЃЌЁЃЌAnЃЈanЃЌ0ЃЉЃЌЁЪЧxжсе§АыжсЩЯЕФЕуЃЌЧвЁїAA1P1ЃЌЁїA1A2P2ЃЌЁЃЌЁїAn-1AnPnЃЌЁОљЮЊаББпдкxжсЩЯЕФЕШбќжБНЧШ§НЧаЮЃЈAЮЊзјБъдЕуЃЉЃЎЃЈ1ЃЉаДГіan-1ЁЂanКЭxnжЎМфЕФЕШСПЙиЯЕЃЌвдМАan-1ЁЂanКЭynжЎМфЕФЕШСПЙиЯЕЃЛ
ЃЈ2ЃЉВТВтВЂжЄУїЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ3ЃЉЩш
 ЃЌМЏКЯB={b1ЃЌb2ЃЌb3ЃЌЁЃЌbnЃЌЁ}ЃЌA={x|x2-2ax+a2-1ЃМ0ЃЌxЁЪR}ЃЌШєAЁЩB=∅ЃЌЧѓЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЃЎ
ЃЌМЏКЯB={b1ЃЌb2ЃЌb3ЃЌЁЃЌbnЃЌЁ}ЃЌA={x|x2-2ax+a2-1ЃМ0ЃЌxЁЪR}ЃЌШєAЁЩB=∅ЃЌЧѓЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЗжЮіЃКЃЈ1ЃЉвРЬтвтРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЃЌ ЃЌ
ЃЌ ЃЎ
ЃЎ
ЃЈ2ЃЉгЩ ЕУ
ЕУ  =
= ЃЌМД
ЃЌМД ЃЌВТВт
ЃЌВТВт ЃЌ
ЃЌ
дйгУЪ§бЇЙщФЩЗЈНјаажЄУїЃЎ
ЃЈ3ЃЉгУСбЯюЗЈЧѓЕУ ЕФжЕЮЊ
ЕФжЕЮЊ ЃЌгЩКЏЪ§
ЃЌгЩКЏЪ§ дкЧјМф
дкЧјМф
[1ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧв ЃЌЧѓЕУ
ЃЌЧѓЕУ ЃЌдйгЩ A={x|x2-2ax+a2-1ЃМ0ЃЌaЁЪR}=
ЃЌдйгЩ A={x|x2-2ax+a2-1ЃМ0ЃЌaЁЪR}=
{x|xЁЪЃЈa-1ЃЌa+1ЃЉ}ЃЌAЁЩB=ІеЃЌгаa+1Ём0ЃЌЛђ ЃЌгЩДЫЧѓЕУЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЃЎ
ЃЌгЩДЫЧѓЕУЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉвРЬтвтРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЃЌ ЃЌ
ЃЌ ЃЎЁЃЈ4ЗжЃЉ
ЃЎЁЃЈ4ЗжЃЉ
ЃЈ2ЃЉгЩ ЕУ
ЕУ  =
= ЃЌ
ЃЌ
МД ЃЌВТВт
ЃЌВТВт ЃЎ ЁЃЈ2ЗжЃЉ
ЃЎ ЁЃЈ2ЗжЃЉ
жЄУїЃКЂйЕБn=1ЪБЃЌПЩЧѓЕУ ЃЌУќЬтГЩСЂЃЎ ЁЃЈ1ЗжЃЉ
ЃЌУќЬтГЩСЂЃЎ ЁЃЈ1ЗжЃЉ
ЂкМйЩшЕБn=kЪБЃЌУќЬтГЩСЂЃЌМДга ЃЌЁЃЈ1ЗжЃЉ
ЃЌЁЃЈ1ЗжЃЉ
дђЕБn=k+1ЪБЃЌгЩЙщФЩМйЩшМА ЃЌ
ЃЌ
ЕУ ЃЌ
ЃЌ
МД
НтЕУ ЃЌЃЈ
ЃЌЃЈ ВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
МДЕБn=k+1ЪБЃЌУќЬтГЩСЂЃЎ ЁЃЈ3ЗжЃЉ
злЩЯЫљЪіЃЌЖдЫљгаnЁЪN*ЃЌ ЃЎ ЁЃЈ1ЗжЃЉ
ЃЎ ЁЃЈ1ЗжЃЉ
ЃЈ3ЃЉ =
= =
= ЃЎЁЃЈ2ЗжЃЉ
ЃЎЁЃЈ2ЗжЃЉ
вђЮЊКЏЪ§ дкЧјМф[1ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧв
дкЧјМф[1ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧв ЃЌ
ЃЌ
Ыљвд ЃЎЁЃЈ2ЗжЃЉ
ЃЎЁЃЈ2ЗжЃЉ
A={x|x2-2ax+a2-1ЃМ0ЃЌaЁЪR}={x|xЁЪЃЈa-1ЃЌa+1ЃЉ}
гЩAЁЩB=ІеЃЌгаa+1Ём0ЃЌЛђ ЃЌ
ЃЌ
ЙЪЃЌ ЃЌМД ЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЮЊ
ЃЌМД ЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЮЊ  ЃЎЁЃЈ2ЗжЃЉ
ЃЎЁЃЈ2ЗжЃЉ
ЕуЦРЃКБОЬтжївЊПМВщЪ§бЇЙщФЩЗЈЕФгІгУЃЌгУСбЯюЗЈЖдЪ§СаЧѓКЭЃЌСНИіМЏКЯЕФНЛМЏЕФЖЈвхЕФгІгУЃЌЪєгкФбЬтЃЎ
 ЃЌ
ЃЌ ЃЎ
ЃЎЃЈ2ЃЉгЩ
 ЕУ
ЕУ  =
= ЃЌМД
ЃЌМД ЃЌВТВт
ЃЌВТВт ЃЌ
ЃЌдйгУЪ§бЇЙщФЩЗЈНјаажЄУїЃЎ
ЃЈ3ЃЉгУСбЯюЗЈЧѓЕУ
 ЕФжЕЮЊ
ЕФжЕЮЊ ЃЌгЩКЏЪ§
ЃЌгЩКЏЪ§ дкЧјМф
дкЧјМф[1ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧв
 ЃЌЧѓЕУ
ЃЌЧѓЕУ ЃЌдйгЩ A={x|x2-2ax+a2-1ЃМ0ЃЌaЁЪR}=
ЃЌдйгЩ A={x|x2-2ax+a2-1ЃМ0ЃЌaЁЪR}={x|xЁЪЃЈa-1ЃЌa+1ЃЉ}ЃЌAЁЩB=ІеЃЌгаa+1Ём0ЃЌЛђ
 ЃЌгЩДЫЧѓЕУЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЃЎ
ЃЌгЩДЫЧѓЕУЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЃЎНтД№ЃКНтЃКЃЈ1ЃЉвРЬтвтРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЃЌ
 ЃЌ
ЃЌ ЃЎЁЃЈ4ЗжЃЉ
ЃЎЁЃЈ4ЗжЃЉЃЈ2ЃЉгЩ
 ЕУ
ЕУ  =
= ЃЌ
ЃЌМД
 ЃЌВТВт
ЃЌВТВт ЃЎ ЁЃЈ2ЗжЃЉ
ЃЎ ЁЃЈ2ЗжЃЉжЄУїЃКЂйЕБn=1ЪБЃЌПЩЧѓЕУ
 ЃЌУќЬтГЩСЂЃЎ ЁЃЈ1ЗжЃЉ
ЃЌУќЬтГЩСЂЃЎ ЁЃЈ1ЗжЃЉЂкМйЩшЕБn=kЪБЃЌУќЬтГЩСЂЃЌМДга
 ЃЌЁЃЈ1ЗжЃЉ
ЃЌЁЃЈ1ЗжЃЉдђЕБn=k+1ЪБЃЌгЩЙщФЩМйЩшМА
 ЃЌ
ЃЌЕУ
 ЃЌ
ЃЌМД

НтЕУ
 ЃЌЃЈ
ЃЌЃЈ ВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ВЛКЯЬтвтЃЌЩсШЅЃЉЃЌМДЕБn=k+1ЪБЃЌУќЬтГЩСЂЃЎ ЁЃЈ3ЗжЃЉ
злЩЯЫљЪіЃЌЖдЫљгаnЁЪN*ЃЌ
 ЃЎ ЁЃЈ1ЗжЃЉ
ЃЎ ЁЃЈ1ЗжЃЉЃЈ3ЃЉ
 =
= =
= ЃЎЁЃЈ2ЗжЃЉ
ЃЎЁЃЈ2ЗжЃЉвђЮЊКЏЪ§
 дкЧјМф[1ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧв
дкЧјМф[1ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЌЧв ЃЌ
ЃЌЫљвд
 ЃЎЁЃЈ2ЗжЃЉ
ЃЎЁЃЈ2ЗжЃЉA={x|x2-2ax+a2-1ЃМ0ЃЌaЁЪR}={x|xЁЪЃЈa-1ЃЌa+1ЃЉ}
гЩAЁЩB=ІеЃЌгаa+1Ём0ЃЌЛђ
 ЃЌ
ЃЌЙЪЃЌ
 ЃЌМД ЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЮЊ
ЃЌМД ЪЕГЃЪ§aЕФШЁжЕЗЖЮЇЮЊ  ЃЎЁЃЈ2ЗжЃЉ
ЃЎЁЃЈ2ЗжЃЉЕуЦРЃКБОЬтжївЊПМВщЪ§бЇЙщФЩЗЈЕФгІгУЃЌгУСбЯюЗЈЖдЪ§СаЧѓКЭЃЌСНИіМЏКЯЕФНЛМЏЕФЖЈвхЕФгІгУЃЌЪєгкФбЬтЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
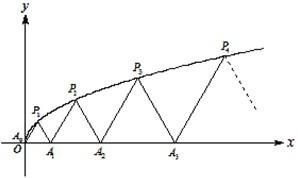 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ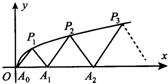 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎдђa1=
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎдђa1=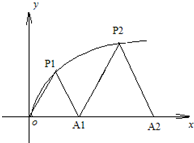 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉ ЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉ ЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ ЃЈ2012•еЂББЧјЖўФЃЃЉШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЌЁЪЧЧњЯп
ЃЈ2012•еЂББЧјЖўФЃЃЉШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЌЁЪЧЧњЯп