题目内容
已知双曲线C的离心率为
,且过点(4,-
)
(1)求双曲线C的标准方程;
(2)若点M(3,m)在双曲线C上,求证:MF1⊥MF2;
(3)求△F1MF2的面积.
| 2 |
| 10 |
(1)求双曲线C的标准方程;
(2)若点M(3,m)在双曲线C上,求证:MF1⊥MF2;
(3)求△F1MF2的面积.
分析:(1)根据双曲线C的离心率为
,得出双曲线为等轴双曲线,从而设双曲线C的方程为nx2-ny2=1利用双曲线C过点(4,-
)即可求出n的值,最后写出双曲线的方程即可.
(2)先根据点M(3,m)在双曲线C上求出m值,由双曲线的对称性知,我们只需证明点M(3,
) 满足MF1⊥MF2即可,利用向量的数量积等于0即可证得MF1⊥MF2;
(3)利用(2)中的数据结合三角形的面积公式即可求得△F1MF2的面积.
| 2 |
| 10 |
(2)先根据点M(3,m)在双曲线C上求出m值,由双曲线的对称性知,我们只需证明点M(3,
| 3 |
(3)利用(2)中的数据结合三角形的面积公式即可求得△F1MF2的面积.
解答:解:(1)∵双曲线C的离心率为
,
∴双曲线为等轴双曲线
∴设双曲线C的方程为nx2-ny2=1
∵双曲线C过点(4,-
)
∴16n-10n=1∴n=
∴
-
=1即为所求.
(2)∵点M(3,m)在双曲线C上
∴m=±
由双曲线的对称性知,我们只需证明点M(3,
) 满足MF1⊥MF2即可
∴
=(2
-3,-
),
=(-2
-3,-
)
∴
•
=(2
-3)(-2
-3)+(-
)(-
)=0,
∴MF1⊥MF2;
(3)S△F1MF2=
|
||
|
=
•
=
=6.
| 2 |
∴双曲线为等轴双曲线
∴设双曲线C的方程为nx2-ny2=1
∵双曲线C过点(4,-
| 10 |
∴16n-10n=1∴n=
| 1 |
| 6 |
∴
| x2 |
| 6 |
| y2 |
| 6 |
(2)∵点M(3,m)在双曲线C上
∴m=±
| 3 |
由双曲线的对称性知,我们只需证明点M(3,
| 3 |
∴
| MF1 |
| 3 |
| 3 |
| MF2 |
| 3 |
| 3 |
∴
| MF1 |
| MF2 |
| 3 |
| 3 |
| 3 |
| 3 |
∴MF1⊥MF2;
(3)S△F1MF2=
| 1 |
| 2 |
| MF1 |
| MF2 |
=
| 1 |
| 2 |
(2
|
(-2
|
=
| 1 |
| 2 |
(24-12
|
=6.
点评:本小题主要考查双曲线的简单性质、向量垂直的应用、三角形的面积等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
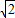 ,且过点(4,-
,且过点(4,-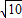 )
)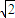 ,且过点(4,-
,且过点(4,-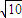 )
)