题目内容
已知a>0且a≠1,函数f(x)=loga(1﹣ax).
(1)求函数f(x)的定义域,并判断f(x)的单调性;
(2)若n∈N+,求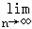
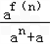 .
.
(1)求函数f(x)的定义域,并判断f(x)的单调性;
(2)若n∈N+,求
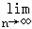
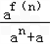 .
.解:(1)∵函数f(x)=loga(1﹣ax),∴1﹣ax>0,∴ax <1.
当 a>1时,由ax <1解得 x<0,定义域为(﹣∞,0).
此时,由于1﹣ax 是(﹣∞,0)上的减函数,
故函数f(x)=loga(1﹣ax)是减函数.
当0<a<1时,由ax <1解得 x>0,定义域为(0,+∞).
此时,由于1﹣ax 是(﹣∞,0)上的增函数,
故函数f(x)=loga(1﹣ax)是减函数.
(2)若n∈N+,因为f(n)=loga(1﹣an),
所以af(n)=1﹣an,由函数定义域知1﹣an>0,
因为n是正整数,故0<a<1,
∴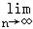
 =
=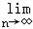
 =
= .
.
当 a>1时,由ax <1解得 x<0,定义域为(﹣∞,0).
此时,由于1﹣ax 是(﹣∞,0)上的减函数,
故函数f(x)=loga(1﹣ax)是减函数.
当0<a<1时,由ax <1解得 x>0,定义域为(0,+∞).
此时,由于1﹣ax 是(﹣∞,0)上的增函数,
故函数f(x)=loga(1﹣ax)是减函数.
(2)若n∈N+,因为f(n)=loga(1﹣an),
所以af(n)=1﹣an,由函数定义域知1﹣an>0,
因为n是正整数,故0<a<1,
∴
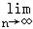
 =
=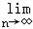
 =
= .
.
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目