题目内容
下列选项中,说法正确的是
- A.命题“?x0∈R,
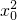 -x0≤0”的否定是“?x∈R,x2-x>0”
-x0≤0”的否定是“?x∈R,x2-x>0” - B.命题“p?q为真”是命题“p∧q为真”的充分不必要条件
- C.命题“若am2≤bm2,则a≤b”是假命题
- D.命题“若sinx=siny,则x=y”的逆否命题为真命题
C
分析:根据“命题的否定”的定义可得A不对;由命题“p?q为真”不能推出命题“p∧q为真”,可得B不对;
通过举反例可得C正确; 求出“若sinx=siny,则x=y”的逆否命题,判断是假命题,故D不对,从而得而出结论.
解答:由于命题“?x0∈R,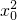 -x0≤0”的否定是“对任意x∈R,x2-x>0”,故A不对.
-x0≤0”的否定是“对任意x∈R,x2-x>0”,故A不对.
由命题“p?q为真”不能推出命题“p∧q为真”,故命题“p?q为真”不是命题“p∧q为真”的充分条件,
故B不对.
由 am2≤bm2 ,不能推出a≤b,例如 由“2×0≤1×0”不能推出“2≤1”,
故“若am2≤bm2,则a≤b”是假命题,故C正确.
由于“若sinx=siny,则x=y”的逆否命题为“若x≠y 则 sinx≠siny”,显然是假命题,故D不对.
故选C.
点评:本题主要考查命题的真假的判断,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于基础题.
分析:根据“命题的否定”的定义可得A不对;由命题“p?q为真”不能推出命题“p∧q为真”,可得B不对;
通过举反例可得C正确; 求出“若sinx=siny,则x=y”的逆否命题,判断是假命题,故D不对,从而得而出结论.
解答:由于命题“?x0∈R,
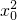 -x0≤0”的否定是“对任意x∈R,x2-x>0”,故A不对.
-x0≤0”的否定是“对任意x∈R,x2-x>0”,故A不对.由命题“p?q为真”不能推出命题“p∧q为真”,故命题“p?q为真”不是命题“p∧q为真”的充分条件,
故B不对.
由 am2≤bm2 ,不能推出a≤b,例如 由“2×0≤1×0”不能推出“2≤1”,
故“若am2≤bm2,则a≤b”是假命题,故C正确.
由于“若sinx=siny,则x=y”的逆否命题为“若x≠y 则 sinx≠siny”,显然是假命题,故D不对.
故选C.
点评:本题主要考查命题的真假的判断,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于基础题.

练习册系列答案
相关题目
 ”的否定是“
”的否定是“ ”
” 满足
满足 ,则
,则 与
与 的夹角为钝角
的夹角为钝角 ,则
,则
 为真”是命题“
为真”是命题“ 为真”的必要不充分条件
为真”的必要不充分条件 ”的否定是“
”的否定是“ ”
” 为真”是命题“
为真”是命题“ 为真”的充分不必要条件
为真”的充分不必要条件 ,则
,则 ”是假命题
”是假命题 ,则
,则 ”的逆否命题为真命题
”的逆否命题为真命题