题目内容
在数列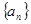 中,已知
中,已知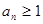 ,
,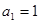 ,且
,且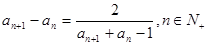 .
.
(1)记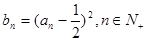 ,求证:数列
,求证:数列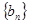 是等差数列;
是等差数列;
(2)求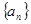 的通项公式;
的通项公式;
(3)对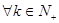 , 是否总
, 是否总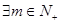 使得
使得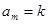 ?若存在,求出
?若存在,求出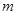 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
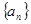 中,已知
中,已知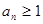 ,
,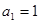 ,且
,且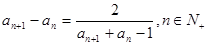 .
.(1)记
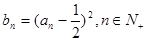 ,求证:数列
,求证:数列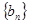 是等差数列;
是等差数列;(2)求
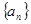 的通项公式;
的通项公式;(3)对
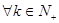 , 是否总
, 是否总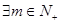 使得
使得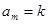 ?若存在,求出
?若存在,求出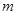 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)见解析;(2)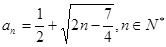 ;(3)存在
;(3)存在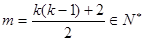
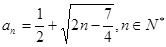 ;(3)存在
;(3)存在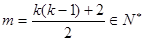
(I)根据等差数列的定义可得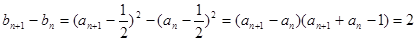 问题到此基本得到解决.
问题到此基本得到解决.
(II)由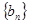 的通项公式进而可求得
的通项公式进而可求得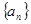 的通项公式.
的通项公式.
(III)本小题是探索性问题,可假设存在,则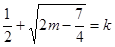 ,
,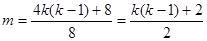 ,而
,而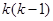 总为偶数且非负,
总为偶数且非负,
进而可知是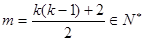 存在的.
存在的.
解:(1)由题意得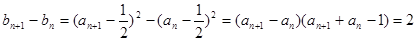
又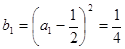 ,故
,故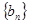 是以
是以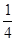 为首项,以2为公差的等差数列; 4分
为首项,以2为公差的等差数列; 4分
(2)由(1)得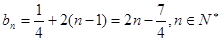
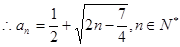 8分
8分
(3)设对任意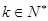 存在
存在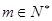 ,使得
,使得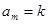 ,
,
即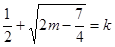
整理得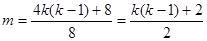 ,而
,而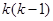 总为偶数且非负,
总为偶数且非负,
故
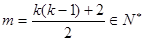 13分
13分
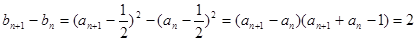 问题到此基本得到解决.
问题到此基本得到解决.(II)由
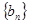 的通项公式进而可求得
的通项公式进而可求得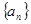 的通项公式.
的通项公式.(III)本小题是探索性问题,可假设存在,则
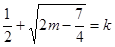 ,
,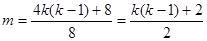 ,而
,而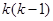 总为偶数且非负,
总为偶数且非负,进而可知是
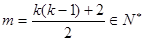 存在的.
存在的.解:(1)由题意得
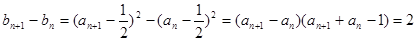
又
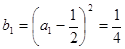 ,故
,故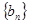 是以
是以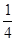 为首项,以2为公差的等差数列; 4分
为首项,以2为公差的等差数列; 4分(2)由(1)得
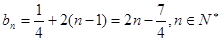
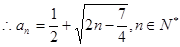 8分
8分(3)设对任意
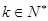 存在
存在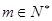 ,使得
,使得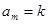 ,
,即
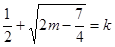
整理得
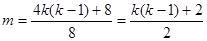 ,而
,而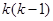 总为偶数且非负,
总为偶数且非负,故
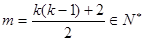 13分
13分
练习册系列答案
相关题目
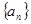 中,
中,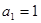 ,
,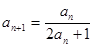 .
.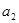 、
、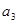 、
、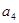 的值;
的值;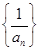 为等差数列.
为等差数列. 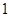 ﹠
﹠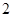 ,
,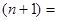
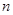
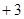 ,则
,则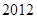 的值为( )
的值为( )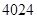
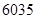
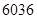
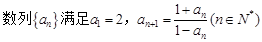 ,则该数列的前2011项的乘积
,则该数列的前2011项的乘积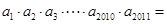 _____________
_____________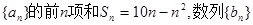 的每一项都有
的每一项都有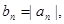 求数列
求数列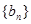 的前n项和
的前n项和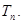
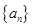 中,若
中,若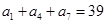 ,,
,, 则前9项和等于( )
则前9项和等于( ) 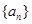 满足
满足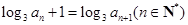 且
且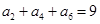 ,则
,则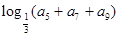 的值是 ( )
的值是 ( )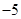
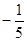
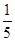
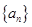 中,若
中,若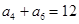 ,
,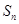 是数列
是数列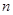 项和,则
项和,则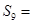 ( )
( )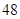
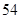
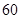
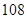
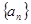 中,有
中,有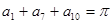 ,则
,则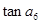 = ▲ 。
= ▲ 。