题目内容
已知函数y=Asin(ωx+φ)+n的最大值为4,最小值是0,最小正周期是 ,直线x=
,直线x= 是其图象的一条对称轴,若A>0,ω>0,0<φ<
是其图象的一条对称轴,若A>0,ω>0,0<φ< ,则函数解析式为 .
,则函数解析式为 .
【答案】分析:利用三角函数的有界性求出最大值、最小值列出方程求出A,n;利用周期公式求出ω,利用整体思想将对称轴代入sin(ωx+φ=)=1或-1,求出φ,求出解析式
解答:解:由题设得,a+n=4,-A+n=0, 得A=2,n=2,ω=4,
得A=2,n=2,ω=4,
且当x= 时,sin(
时,sin( π+φ)=±1,故φ=
π+φ)=±1,故φ= .
.
所求解析式为y=2sin(4x+ )+2.
)+2.
故答案为y=2sin(4x+ )+2
)+2
点评:本题考查三角函数的有界性、周期公式T= 、整体代换的思想求对称性.
、整体代换的思想求对称性.
解答:解:由题设得,a+n=4,-A+n=0,
 得A=2,n=2,ω=4,
得A=2,n=2,ω=4,且当x=
 时,sin(
时,sin( π+φ)=±1,故φ=
π+φ)=±1,故φ= .
.所求解析式为y=2sin(4x+
 )+2.
)+2.故答案为y=2sin(4x+
 )+2
)+2点评:本题考查三角函数的有界性、周期公式T=
 、整体代换的思想求对称性.
、整体代换的思想求对称性. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
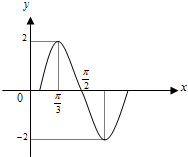 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数