题目内容
已知点M,N的坐标分别为(-2,0),(2,0),直线MP,NP相交于点P,且它们的斜率之积是 ,点P的轨迹记为D.△ABC的顶点A,B在D上,C在直线l:y=x+2上,且AB∥l.
,点P的轨迹记为D.△ABC的顶点A,B在D上,C在直线l:y=x+2上,且AB∥l.
(1)求曲线D的方程;
(2)若AB边通过坐标原点O,求AB的长及△ABC的面积;
(3)若线段AB的垂直平分线与线段BC的垂直平分线交于线段AC的中点,求△ABC的外接圆面积最大时线段AB所在直线的方程.
解;(1)设点P的坐标( x,y),由条件得: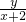 •
•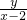 =-1,化简得:曲线D的方程为:x2+y2=4,表示一个圆.
=-1,化简得:曲线D的方程为:x2+y2=4,表示一个圆.
(2)∵点A,B在D上,AB边通过坐标原点O,故AB边是圆的直径,∴AB=4,且AB方程为:y=x,
AB与直线l之间的距离d=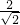 =
=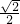 ,△ABC的面积S=
,△ABC的面积S= |AB|•d=
|AB|•d= .
.
(3)∵线段AB的垂直平分线与线段BC的垂直平分线交于线段AC的中点,
∴线段AC的中点是△ABC外接圆的圆心,且AB⊥BC,∴点C还在圆x2+y2=4 上,
外接圆半径r= AC,又AC最大为圆x2+y2=4 的直径4,
AC,又AC最大为圆x2+y2=4 的直径4,
∴r= AC的最大值是2,此时,A(0,-2),C(0,2)
AC的最大值是2,此时,A(0,-2),C(0,2)
AB方程为y+2=1•(x-0),即:x-y-2=0.
分析:(1)直接根据题中条件求曲线D的方程.
(2)坐标原点是曲线D的圆心,故AB边是圆的直径,AB与直线l之间的距离为△ABC的高,,△ABC的面积S= |AB|•d
|AB|•d
(3)圆心在弦的中垂线上,直径对的圆周角等于90度,当所求圆的半径最大时,所求圆的面积最大.
点评:本题主要考查求曲线的方程,综合运用圆的性质,直线和圆的位置关系,属于难题.
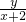 •
•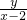 =-1,化简得:曲线D的方程为:x2+y2=4,表示一个圆.
=-1,化简得:曲线D的方程为:x2+y2=4,表示一个圆.(2)∵点A,B在D上,AB边通过坐标原点O,故AB边是圆的直径,∴AB=4,且AB方程为:y=x,
AB与直线l之间的距离d=
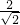 =
=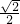 ,△ABC的面积S=
,△ABC的面积S= |AB|•d=
|AB|•d= .
.(3)∵线段AB的垂直平分线与线段BC的垂直平分线交于线段AC的中点,
∴线段AC的中点是△ABC外接圆的圆心,且AB⊥BC,∴点C还在圆x2+y2=4 上,
外接圆半径r=
 AC,又AC最大为圆x2+y2=4 的直径4,
AC,又AC最大为圆x2+y2=4 的直径4,∴r=
 AC的最大值是2,此时,A(0,-2),C(0,2)
AC的最大值是2,此时,A(0,-2),C(0,2)AB方程为y+2=1•(x-0),即:x-y-2=0.
分析:(1)直接根据题中条件求曲线D的方程.
(2)坐标原点是曲线D的圆心,故AB边是圆的直径,AB与直线l之间的距离为△ABC的高,,△ABC的面积S=
 |AB|•d
|AB|•d(3)圆心在弦的中垂线上,直径对的圆周角等于90度,当所求圆的半径最大时,所求圆的面积最大.
点评:本题主要考查求曲线的方程,综合运用圆的性质,直线和圆的位置关系,属于难题.

练习册系列答案
相关题目
 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点M
以F2为焦点且与椭圆相交于点M 、N
、N ,直线
,直线 与抛物线C相切
与抛物线C相切 ,
, .直线
.直线 相交于点M,且它们的斜率之积为-2.
相交于点M,且它们的斜率之积为-2. 的直线
的直线 交动点M的轨迹于C、D两点, 且N为线段CD的中点,求直线
交动点M的轨迹于C、D两点, 且N为线段CD的中点,求直线