题目内容
在等差数列{an}中,若a1+a2+…+a49=0,且公差d≠0,则有
- A.a1+a49>0
- B.a1+a49<0
- C.a3+a47=0
- D.a50=0
C
分析:本题考查的是等差数列的性质,由a1+a2+…+a49=0,结合等差数列前n项和公式,易得a1+a49=0,又等差数列的性质,m+n=p+q,则am+an=ap+aq,不难得到答案.
解答:∵在等差数列{an}中
S49=a1+a2+…+a49
=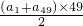
=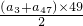 =0
=0
∴a1+a49=a3+a47=0
故选C
点评:由已知条件中a1+a2+…+a49=0,我们不难想到利用等差数列的前n项和公式,对式子的结果进行简化,得a1+a49=0,再结合等差数列的性质,进行求解.故等差数列的性质:m+n=p+q,则am+an=ap+aq,是解决本题的关键.
分析:本题考查的是等差数列的性质,由a1+a2+…+a49=0,结合等差数列前n项和公式,易得a1+a49=0,又等差数列的性质,m+n=p+q,则am+an=ap+aq,不难得到答案.
解答:∵在等差数列{an}中
S49=a1+a2+…+a49
=
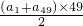
=
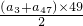 =0
=0∴a1+a49=a3+a47=0
故选C
点评:由已知条件中a1+a2+…+a49=0,我们不难想到利用等差数列的前n项和公式,对式子的结果进行简化,得a1+a49=0,再结合等差数列的性质,进行求解.故等差数列的性质:m+n=p+q,则am+an=ap+aq,是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目