题目内容
已知椭圆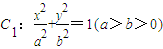 的左右焦点分别为F1,F2,O为坐标原点,过F2的直线l1与C1交于A,B两点,且△ABF1的周长为
的左右焦点分别为F1,F2,O为坐标原点,过F2的直线l1与C1交于A,B两点,且△ABF1的周长为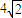 ,l1的倾斜角为α.
,l1的倾斜角为α.(I)当l1垂直于x轴时,
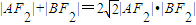
①求椭圆C1的方程;
②求证:对于?α∈[0,π),总有
 .
.(II)在(I)的条件下,设直线l2与椭圆交于C,D两点,且OC⊥OD,过O作l2的垂线交l2于E,求E的轨迹方程C2,并比较C2与C1通径所在直线的位置关系.
【答案】分析:(I)由题意可得, ,当斜率不存在时,l1:x=c,
,当斜率不存在时,l1:x=c, ,
, ;当
;当 时,设l1:y=k(x-1),A(x1,y1),B(x2,y2),由焦半径公式可得,
时,设l1:y=k(x-1),A(x1,y1),B(x2,y2),由焦半径公式可得, ,故
,故 .由此能导出对于?α∈[0,π),总有
.由此能导出对于?α∈[0,π),总有 .
.
(II)当斜率存在时,设l2:y=tx+b,C(x3,y3),D(x4,y4), ,
, ,再由根的判别式和韦达定理进行求解.
,再由根的判别式和韦达定理进行求解.
解答:解:(I)①由题意可得,
当斜率不存在时,l1:x=c
故 ,
,
②当 时,设l1:y=k(x-1),A(x1,y1),B(x2,y2)
时,设l1:y=k(x-1),A(x1,y1),B(x2,y2)
由焦半径公式可得,
故 ,
,

 ,
,
故
故 成立
成立
当 时,由题意成立
时,由题意成立
故对于?α∈[0,π),总有 .
.
(II)当斜率存在时,设l2:y=tx+b,C(x3,y3),D(x4,y4)
 ,
,
△>0⇒2t2-b2+1>0
故 ,
,
原点O到l2的距离为 为定值
为定值
故E的轨迹方程为 ,
,
当斜率不存在时,解得 或
或 均在E上
均在E上
综上可得,E的轨迹方程C2为 ,
,
C1通径所在的方程为x=±1
故两者相离.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用椭圆性质,注意合理地进行等价转化.
 ,当斜率不存在时,l1:x=c,
,当斜率不存在时,l1:x=c, ,
, ;当
;当 时,设l1:y=k(x-1),A(x1,y1),B(x2,y2),由焦半径公式可得,
时,设l1:y=k(x-1),A(x1,y1),B(x2,y2),由焦半径公式可得, ,故
,故 .由此能导出对于?α∈[0,π),总有
.由此能导出对于?α∈[0,π),总有 .
.(II)当斜率存在时,设l2:y=tx+b,C(x3,y3),D(x4,y4),
 ,
, ,再由根的判别式和韦达定理进行求解.
,再由根的判别式和韦达定理进行求解.解答:解:(I)①由题意可得,

当斜率不存在时,l1:x=c

故
 ,
,②当
 时,设l1:y=k(x-1),A(x1,y1),B(x2,y2)
时,设l1:y=k(x-1),A(x1,y1),B(x2,y2)由焦半径公式可得,

故
 ,
,
 ,
,故

故
 成立
成立当
 时,由题意成立
时,由题意成立故对于?α∈[0,π),总有
 .
.(II)当斜率存在时,设l2:y=tx+b,C(x3,y3),D(x4,y4)

 ,
,△>0⇒2t2-b2+1>0

故
 ,
,原点O到l2的距离为
 为定值
为定值故E的轨迹方程为
 ,
,当斜率不存在时,解得
 或
或 均在E上
均在E上综上可得,E的轨迹方程C2为
 ,
,C1通径所在的方程为x=±1
故两者相离.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用椭圆性质,注意合理地进行等价转化.

练习册系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点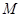 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.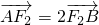 ,求k的值.
,求k的值. 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆