题目内容
20.通常用![]() 分别表示△
分别表示△![]() 的三个内角
的三个内角![]() 所对边的边长,
所对边的边长,![]() 表示△
表示△![]() 的外接圆半径.
的外接圆半径.
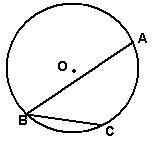
(1) 如图,在以![]() 为圆心、半径为2的⊙
为圆心、半径为2的⊙![]() 中,
中,![]() 和
和![]() 是⊙
是⊙![]() 的弦,其中
的弦,其中![]() ,
,![]() ,求弦
,求弦![]() 的长;
的长;
(2) 在△![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(3) 给定三个正实数![]() ,其中
,其中![]() . 问:
. 问:![]() 满足怎样的关系时,以
满足怎样的关系时,以![]() 为边长,
为边长,![]() 为外接圆半径的△
为外接圆半径的△![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在△
不存在、存在一个或存在两个(全等的三角形算作同一个)?在△![]() 存在的情况下,用
存在的情况下,用![]() 表示
表示![]() .
.
[解] (1) △![]() 的外接圆半径为2,在△
的外接圆半径为2,在△![]() 中,
中,![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.

[证明] (2) ![]() ,由于
,由于![]() 是钝角,
是钝角,![]() 都是锐角,得
都是锐角,得![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,即
,即![]() .
.
[解](3)ⅰ)当![]() 或
或![]() 时,所求的△
时,所求的△![]() 不存在.
不存在.
ⅱ)当![]() 且
且![]() 时,
时,![]() ,所求的△
,所求的△![]() 只存在一个,且
只存在一个,且![]() .
.
ⅲ)当![]() 且
且![]() 时,
时,![]() ,且
,且![]() 都是锐角,由
都是锐角,由![]() ,
,![]() 唯一确定.
唯一确定.
因此,所求的△![]() 只存在一个,且
只存在一个,且![]() .
.
ⅳ)当![]() 时,
时,![]() 总是锐角,
总是锐角,![]() 可以是钝角也可以是锐角,因此,所求的△
可以是钝角也可以是锐角,因此,所求的△![]() 存在两个. 由
存在两个. 由![]() ,
,![]() ,得
,得
当![]() 时,
时,![]() ,
,
![]()
![]() .
.
当![]() 时,
时,![]() ,
,
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目