题目内容
下面四个命题:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②把函数y=3sin(2x+ )的图象向右平移
)的图象向右平移 个单位,得到y=3sin2x的图象;
个单位,得到y=3sin2x的图象;
③函数f(x)=ax2-lnx的图象在x=1处的切线平行于直线y=x,则( ,+∞)是f(x)的单调递增区间;
,+∞)是f(x)的单调递增区间;
④正方体的内切球与其外接球的表面积之比为1:3;
其中所有正确命题的序号为________.
①③④
分析:根据含有量词的命题的否定的方法,得到①正确;根据函数图象平移的规律,得到②错误;根据导数的几何意义,结合利用导数判断函数单调性的方法,得到③正确;根据正方体的结构特征,结合球的表面积公式,得到④正确.
解答:对于①,它是一个含有量词的命题
“?x∈R,x2-x>0”即“存在x∈R,使得x2-x>0成立”,其否定应该是不存在满足条件的x.
也就是说,对于任意的x∈R,都有x2-x≤0,即“?x∈R,x2-x≤0”,故①正确;
对于②,设F(x)=3sin(2x+ ),图象向右平移
),图象向右平移 个单位,应该得到F(x-
个单位,应该得到F(x- )=3sin(2x-
)=3sin(2x- ),
),
而不是y=3sin2x的图象,故②错误;
对于③,若函数f(x)=ax2-lnx的图象在x=1处的切线平行于直线y=x,
说明f′(1)=1,而
所以2a-1=1,得a=1,函数表达式为f(x)=x2-lnx
∴ ,当x∈(
,当x∈( ,+∞),f′(x)>0,函数为增函数,故③正确;
,+∞),f′(x)>0,函数为增函数,故③正确;
对于④,设正方体的棱长为a,则它的内切球半径为 ,表面积为
,表面积为 =4πa2,
=4πa2,
而正方体的外接球半径为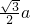 ,可得外接球的表面积为
,可得外接球的表面积为 =12πa2
=12πa2
∴内切球与其外接球的表面积之比为1:3,故④正确
故答案为:①③④
点评:本题综合了含有量词的命题的否定、导数的几何意义、运用导数判断函数的单调性和球的内接外切等知识点,考查了命题真假的判断,属于中档题.
分析:根据含有量词的命题的否定的方法,得到①正确;根据函数图象平移的规律,得到②错误;根据导数的几何意义,结合利用导数判断函数单调性的方法,得到③正确;根据正方体的结构特征,结合球的表面积公式,得到④正确.
解答:对于①,它是一个含有量词的命题
“?x∈R,x2-x>0”即“存在x∈R,使得x2-x>0成立”,其否定应该是不存在满足条件的x.
也就是说,对于任意的x∈R,都有x2-x≤0,即“?x∈R,x2-x≤0”,故①正确;
对于②,设F(x)=3sin(2x+
 ),图象向右平移
),图象向右平移 个单位,应该得到F(x-
个单位,应该得到F(x- )=3sin(2x-
)=3sin(2x- ),
),而不是y=3sin2x的图象,故②错误;
对于③,若函数f(x)=ax2-lnx的图象在x=1处的切线平行于直线y=x,
说明f′(1)=1,而

所以2a-1=1,得a=1,函数表达式为f(x)=x2-lnx
∴
 ,当x∈(
,当x∈( ,+∞),f′(x)>0,函数为增函数,故③正确;
,+∞),f′(x)>0,函数为增函数,故③正确;对于④,设正方体的棱长为a,则它的内切球半径为
 ,表面积为
,表面积为 =4πa2,
=4πa2,而正方体的外接球半径为
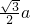 ,可得外接球的表面积为
,可得外接球的表面积为 =12πa2
=12πa2∴内切球与其外接球的表面积之比为1:3,故④正确
故答案为:①③④
点评:本题综合了含有量词的命题的否定、导数的几何意义、运用导数判断函数的单调性和球的内接外切等知识点,考查了命题真假的判断,属于中档题.

练习册系列答案
相关题目
 是a,b,c三个数成等比数列的既不充分又非必要条件;
是a,b,c三个数成等比数列的既不充分又非必要条件; 是a,b,c三个数成等比数列的既不充分又非必要条件;
是a,b,c三个数成等比数列的既不充分又非必要条件;