题目内容
设a,b为正实数,下列结论正确的是( )
①若a2-b2=1,则a-b<1;
②若
-
=1,则a-b<1;
③若|
-
|=1,则|a-b|<1;
④若|a3-b3|=1,则|a-b|<1.
①若a2-b2=1,则a-b<1;
②若
| 1 |
| b |
| 1 |
| a |
③若|
| a |
| b |
④若|a3-b3|=1,则|a-b|<1.
分析:①将a2-b2=1,分解变形为(a+1)(a-1)=b2,即可证明a-1<b,即a-b<1;②③可通过举反例的方法证明其错误性;④若a>b,去掉绝对值,将a3-b3=1分解变形为(a-1)(a2+1+a)=b3,即可证明a-b<1,同理当a<b时也可证明b-a<1,从而命题④正确.
解答:解:①若a2-b2=1,则a2-1=b2,即(a+1)(a-1)=b2,
∵a+1>a-1,∴a-1<b,即a-b<1,①正确; ②若若
-
=1,可取a=7,b=
,则a-b>1,∴②错误;
③若若|
-
|=1,则可取a=9,b=4,而|a-b|=5>1,∴③错误;
④由|a3-b3|=1,
若a>b,则a3-b3=1,即a3-1=b3,即(a-1)(a2+1+a)=b3,
∵a2+1+a>b2,∴a-1<b,即a-b<1
若a<b,则b3-a3=1,即b3-1=a3,即(b-1)(b2+1+b)=a3,
∵b2+1+b>a2,∴b-1<a,即b-a<1
∴|a-b|<1∴④正确;
所以正确的答案为①④.
故选D.
∵a+1>a-1,∴a-1<b,即a-b<1,①正确; ②若若
| 1 |
| b |
| 1 |
| a |
| 7 |
| 8 |
③若若|
| a |
| b |
④由|a3-b3|=1,
若a>b,则a3-b3=1,即a3-1=b3,即(a-1)(a2+1+a)=b3,
∵a2+1+a>b2,∴a-1<b,即a-b<1
若a<b,则b3-a3=1,即b3-1=a3,即(b-1)(b2+1+b)=a3,
∵b2+1+b>a2,∴b-1<a,即b-a<1
∴|a-b|<1∴④正确;
所以正确的答案为①④.
故选D.
点评:本题主要考查了不等式的证明方法,间接证明和直接证明的方法,放缩法和举反例法证明不等式,演绎推理能力,有一定难度,属中档题

练习册系列答案
相关题目
从A,B,C,D四个中选做2个,每题10分,共20分
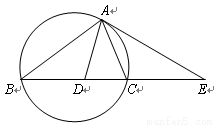
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。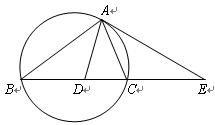 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 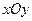 中,设椭圆 中,设椭圆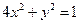 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 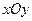 中,点 中,点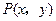 是椭圆 是椭圆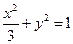 上的一个动点,求 上的一个动点,求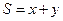 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
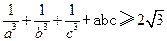 。
。  (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
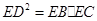 。
。
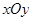 中,设椭圆
中,设椭圆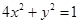 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。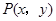 是椭圆
是椭圆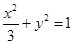 上的一个动点,求
上的一个动点,求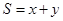 的最大值。
的最大值。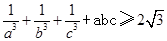 。
。