��Ŀ����
���ڶ���������D�ϵĺ���f��x���������ڱ�����[a��b]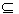 D�ͳ���c��ʹ�ö�����x1��[a��b]������f��x1��=c���Ҷ�����x2��D����x2
D�ͳ���c��ʹ�ö�����x1��[a��b]������f��x1��=c���Ҷ�����x2��D����x2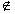 [a��b]ʱ��f��x2����c���������ƺ���f��x��Ϊ����D�ϵġ�ƽ���͡�������
[a��b]ʱ��f��x2����c���������ƺ���f��x��Ϊ����D�ϵġ�ƽ���͡�������
��1���ж�f1��x��=|x��1|+|x��2|��f2��x��=x+|x��2|�Ƿ�ΪR�ϵġ�ƽ���͡���������˵�����ɣ�
��2��������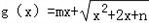 ������[��2��+�ޣ��ϵġ�ƽ���͡���������m��n��ֵ��
������[��2��+�ޣ��ϵġ�ƽ���͡���������m��n��ֵ��
�⣺��1�����ں���f1��x��=|x��1|+|x��2|��
��x��[1��2]ʱ��f1��x��=1��
��x��1��x��2ʱ��f1��x����|��x��1������x��2��|=1�������
��f1��x���ǡ�ƽ���͡�������
���ں���f2��x��=x+|x��2|��
��x�ʣ����ޣ�2]ʱ��f2��x��=2��
��x�ʣ�2��+�ޣ�ʱ��f2��x��=2x��2��2��
���Բ����ڱ�����[a��b]��ʹ��x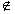 [a��b]ʱ��f��x����2�������
[a��b]ʱ��f��x����2�������
��f2��x�����ǡ�ƽ���͡�������
��2���ɡ�ƽ���͡���������֪�����ڱ�����[a��b]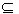 [��2��+�ޣ��ͳ���c��
[��2��+�ޣ��ͳ���c��
ʹ�ö������x��[a��b]��
����g��x��=mx+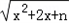 =c��
=c��
�� =c��mx
=c��mx
����x2+2x+n=��c��mx��2 �������
��x2+2x+n=m2x2��2cmx+c2�������x��[a��b]����
����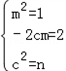 ��
��
����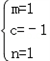 ��
��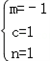
�ٵ�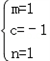 ʱ��g��x��=x+|x+1|��
ʱ��g��x��=x+|x+1|��
��x��[��2����1]ʱ��g��x��=��1��
��x�ʣ���1��+�ޣ�ʱ��g��x��=2x+1����1�������
��ʱ��g��x��������[��2��+�ޣ��ϵġ�ƽ���͡�����
�ڵ�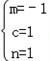 ʱ��g��x��=��x+|x+1|��
ʱ��g��x��=��x+|x+1|��
��x��[��2����1]ʱ��g��x��=��2x��1��1��
��x�ʣ���1��+�ޣ�ʱ��g��x��=1��
��ʱ��g��x����������[��2��+�ޣ��ϵġ�ƽ���͡�������
���Ϸ�����m=1��n=1Ϊ����
��x��[1��2]ʱ��f1��x��=1��
��x��1��x��2ʱ��f1��x����|��x��1������x��2��|=1�������
��f1��x���ǡ�ƽ���͡�������
���ں���f2��x��=x+|x��2|��
��x�ʣ����ޣ�2]ʱ��f2��x��=2��
��x�ʣ�2��+�ޣ�ʱ��f2��x��=2x��2��2��
���Բ����ڱ�����[a��b]��ʹ��x
 [a��b]ʱ��f��x����2�������
[a��b]ʱ��f��x����2���������f2��x�����ǡ�ƽ���͡�������
��2���ɡ�ƽ���͡���������֪�����ڱ�����[a��b]
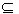 [��2��+�ޣ��ͳ���c��
[��2��+�ޣ��ͳ���c��ʹ�ö������x��[a��b]��
����g��x��=mx+
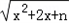 =c��
=c����
 =c��mx
=c��mx����x2+2x+n=��c��mx��2 �������
��x2+2x+n=m2x2��2cmx+c2�������x��[a��b]����
����
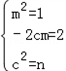 ��
������
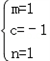 ��
��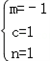
�ٵ�
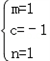 ʱ��g��x��=x+|x+1|��
ʱ��g��x��=x+|x+1|����x��[��2����1]ʱ��g��x��=��1��
��x�ʣ���1��+�ޣ�ʱ��g��x��=2x+1����1�������
��ʱ��g��x��������[��2��+�ޣ��ϵġ�ƽ���͡�����
�ڵ�
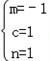 ʱ��g��x��=��x+|x+1|��
ʱ��g��x��=��x+|x+1|����x��[��2����1]ʱ��g��x��=��2x��1��1��
��x�ʣ���1��+�ޣ�ʱ��g��x��=1��
��ʱ��g��x����������[��2��+�ޣ��ϵġ�ƽ���͡�������
���Ϸ�����m=1��n=1Ϊ����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ