Question

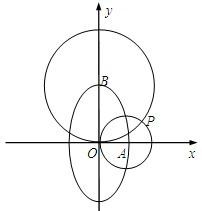如图，设椭圆

y2

a2

+

x2

b2

=1(a＞b＞0)的右顶点与上顶点分别为A、B，以A为圆心，OA为半径的圆与以B为圆心，OB为半径的圆相交于点O、P．
（1）若点P在直线y=

3

2

x上，求椭圆的离心率；
（2）在（1）的条件下，设M是椭圆上的一动点，且点N（0，1）到椭圆上点的最近距离为3，求椭圆的方程．

Answer 1

分析：（1）根据OP是圆A、圆B的公共弦，可推断出OP⊥AB，进而可知k_AB•k_OP=-1，进而求得b和a的关系，进而根据a2-c2=

3

4

a2求得a和c关系，求得离心率．
（2）把点M代入椭圆方程，进而根据（1）中a和b的关系，表示出|MN|，进而看当a≥4和0＜a＜4，分别求得函数取最小值时，求得a，则b可求，椭圆的方程可得．

解答：解：（1）因OP是圆A、圆B的公共弦，
所以OP⊥AB，即k_AB•k_OP=-1，
所以kAB=-

2

3

，又kAB=-

a

b

，
所以b2=

3

4

a2，
所以a2-c2=

3

4

a2?e=

c

a

=

1

2

；
（2）由（1）有b2=

3

4

a2，
所以此时所求椭圆方程为

y2

a2

+

4x2

3a2

=1，
设M（x，y）是椭圆上一点，
则|MN|²=x²+（y-1）²
=

3

4

a2-

3

4

y2+y2-2y+1=

1

4

(y-4)2-3+

3

4

a2，
其中-a≤y≤a，
1°若0＜a＜4时，则当y=a时，|MN|²有最小值a²-2a+1，
由a²-2a+1=9得a=-2或a=4（都舍去）；
2°若a≥4时，则当y=4时，|MN|²有最小值

3

4

a2-3，
由

3

4

a2-3=9得a=±4（舍去负值）即a=4；
综上所述，所求椭圆的方程为

y2

16

+

x2

12

=1．

点评：本题主要考查了椭圆的简单性质．应熟练掌握椭圆方程中，a，b和c关系，做题时才能游刃有余．