Question

在正方体ABCD—A₁B₁C₁D₁中,O为正方形ABCD的中心,M为D₁D的中点.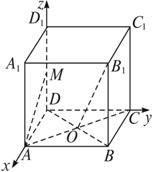

 

(1)求证:异面直线B₁O与AM垂直;

(2)求二面角B₁-AM-C的大小;

(3)若正方体的棱长为a,求三棱锥B₁—AMC的体积.

Answer 1

思路解析:本题的(1)、(2)有两种解法、分别是常规方法和向量法.问题(3)用常规法即可.

解法一:(1)设AD的中点为N、连结ON,由O为正方形ABCD的中心,

得ON⊥平面ADD₁A₁.

又AA₁⊥平面ADD₁A₁、所以A₁N为B₁O在平面ADD₁A₁内的射影.

在正方形ADD₁A₁中,

Rt△A₁AN≌Rt△ADM,∠AA₁N=∠MAD,

∠AA₁N+∠A₁AM=,A₁N⊥AM,

所以B₁O⊥AM.

(2)因为AC⊥平面BB₁D₁D、所以AC⊥B₁O.

由(1),知B₁O⊥AM,所以B₁O⊥AM.

所以B₁O⊥平面AMC.

作OG⊥AM于G,连结B₁G,则∠B₁GO为二面角B₁-AM-C的平面角.

设正方体棱长为1,则OG=

所以tan∠B₁GO=

所以∠B₁GO=arctan.

(3)由(1),知B₁O⊥平面AMC.所以V_B1—AMC=B₁O×S_△AMC.

因棱长为a,所以B₁O=a,

S_△AMC=×MO×AC=

故V_B1—AMC=

解法二:以D为原点、DA所在直线为x轴、DC所在直线为y轴、

DD₁所在直线为z轴、建立空间直角坐标系.

设正方体棱长为2,则M(0,0,1),O(1,1,0),A(2,0,0),B₁(2,2,2).

(1)因OB₁=(1,1,2), =(-2、0、1)、

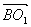·=(1,1,2)·(-2,0,1)=1×(-2)+2×1=0,

所以AM⊥OB₁.

(2)由(1)知AM⊥OB₁、仿(1)可证CM⊥OB₁,

故OB₁⊥面AMC.

又取BC中点为N(1,2,0),A₁(2,0,2), =(-1,2,-2), =(0,2,2),

·=(-1、2、-2)·(0、2、2)=0、

·=(-1、2、-2)·(-2、0、1)=0.

所以A₁N⊥面AB₁M.

于是二面角B₁-AM-C的平面角大小由A₁N与OB₁所成角确定、设其为θ.

cosθ=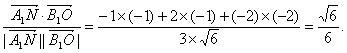

(3)同解法一的(3).