题目内容
已知函数f(x)=
x3+
(1+a)x2+(a+b)x+a有两个极值点x1,x2,且0<x1<1<x2<2,则
的取值范围为( )
| 1 |
| 3 |
| 1 |
| 2 |
| b |
| a |
分析:对函数求导,根据函数有两个极值点得到导函数有两个根,根据导函数的两个根的范围建立a、b的约束条件,然后利用线性规划的方法求出目标函数的取值范围.
解答:解:∵函数f(x)=
x3+
(1+a)x2+(a+b)x+a
∴f′(x)=x2+(a+1)x+(a+b)=0的两个根为x1,x2,
∵x1,x2分别满足0<x1<1<x2<2,
∴
即
画出区域图得
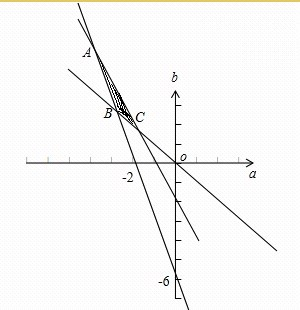
∵
表示可行域内的点与原点连线的斜率,
∴当直线过A点时,直线的斜率取得最小值-
,
当直线过B点时,直线的斜率取得最大值-1,
∴要求的目标函数的范围是[-
,-1]
故选B
| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2+(a+1)x+(a+b)=0的两个根为x1,x2,
∵x1,x2分别满足0<x1<1<x2<2,
∴
|
即
|
画出区域图得

∵
| b |
| a |
∴当直线过A点时,直线的斜率取得最小值-
| 3 |
| 2 |
当直线过B点时,直线的斜率取得最大值-1,
∴要求的目标函数的范围是[-
| 3 |
| 2 |
故选B
点评:本题考查函数的极值取得的条件,考查一元二次方程的实根分布,本题的解题的关键是把问题转化为平面区域内求目标函数的最值问题,本题是一个综合题目.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目