Question

(1)求椭圆的内接矩形的最大面积;

(2)已知矩形ABCD中,点C坐标为(4,4),A点在曲线x²+y²=9(x＞0,y＞0)上移动,且AB、AD两边始终分别平行于x、y坐标轴,求矩形面积ABCD最小时点A的坐标.

Answer 1

解:(1)设内接矩形在第一象限内的顶点为P(acosθ,bsinθ),则有?

S_内接矩形=4S_矩形AOBP=4·acosθ·bsinθ=2absin2θ.?

∵θ∈［0,］,∴2θ∈［0,π］.?

∴S_内接矩形的最大值为2ab.?

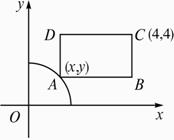
(2)如图所示,设A(x,y),又设矩形ABCD的面积为S,则有S=(4-x)(4-y)=16-4(x+y)+xy.?

∵A(x,y)在曲线x²+y²=9上,?

∴x²+y²=(x+y)²-2xy=9.?

∴xy=

∴S=16-4(x+y)+

=［(x+y)-4］²+.?

又∵x=3cosθ,y=3sinθ(0＜θ＜),?

∴x+y=3(cosθ+sinθ)=32sin(θ+).?

∵＜θ+＜,∴3＜x+y≤3.?

∴当x+y=4时,S有最小值.?

解方程组

∴A点坐标为()或().